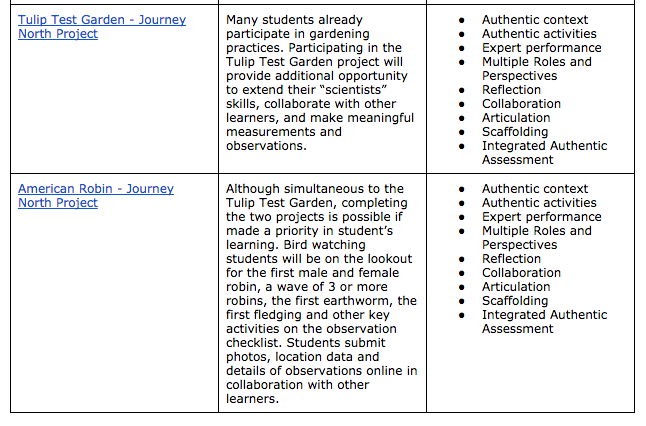
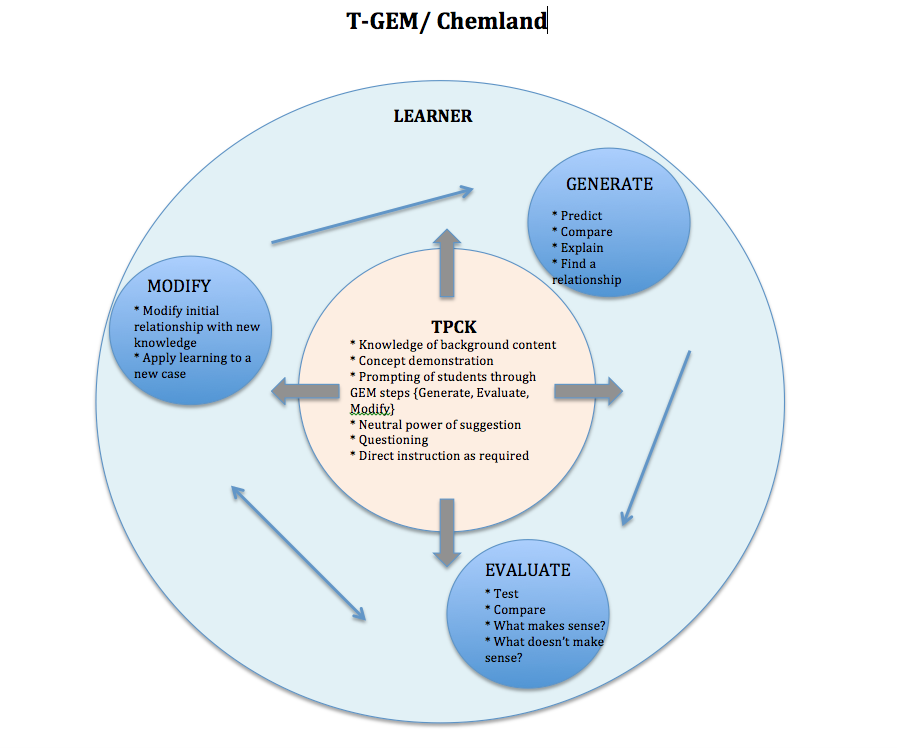
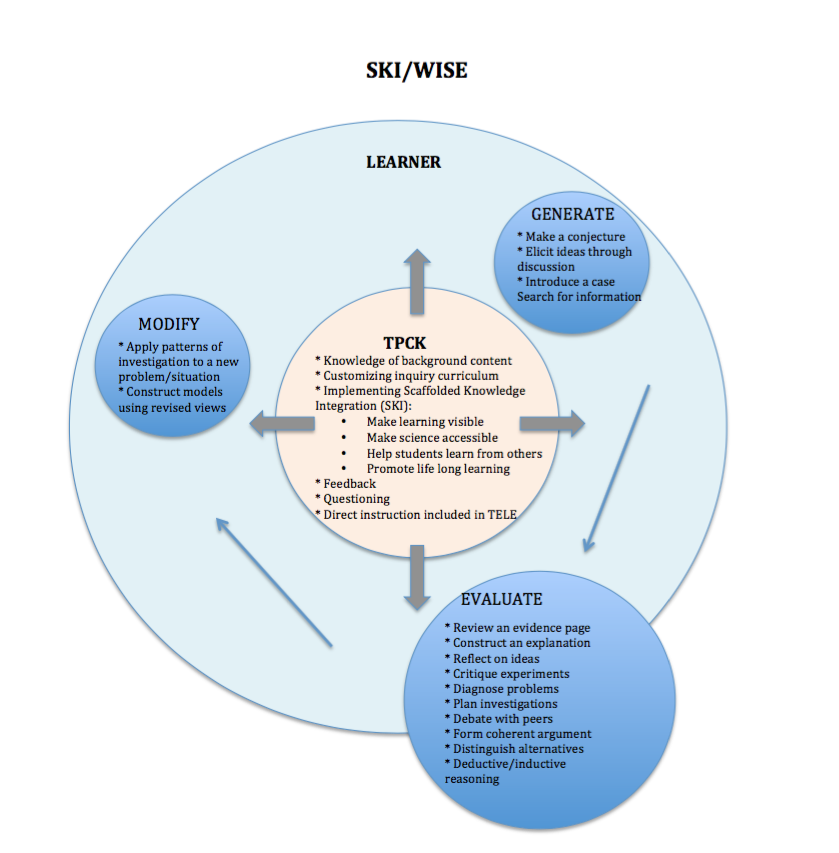
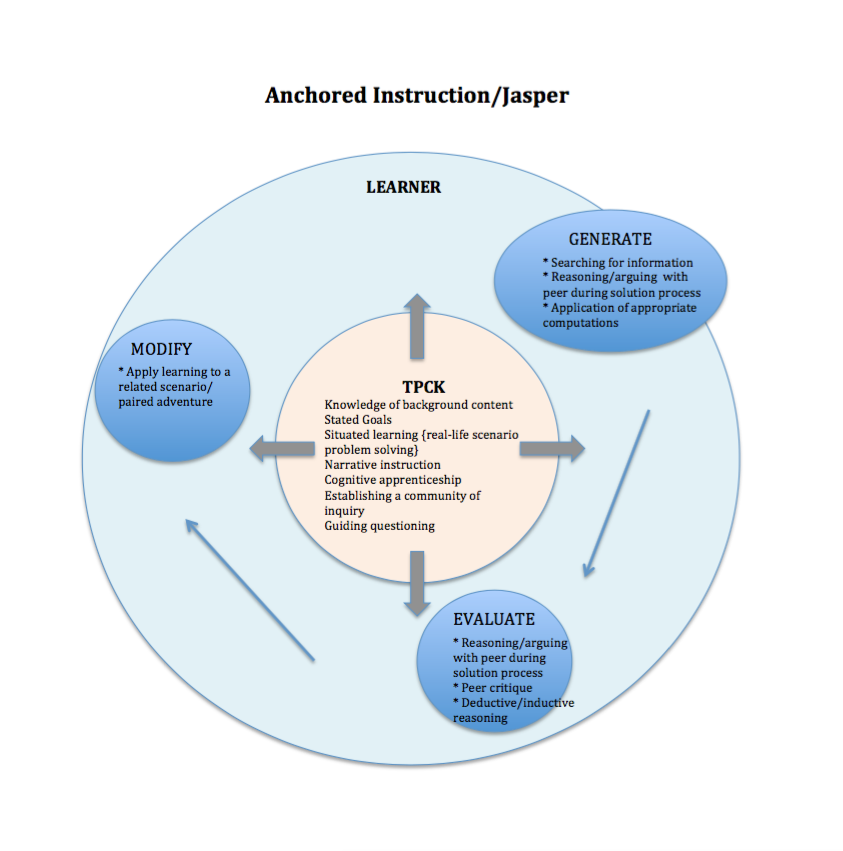
Throughout this MET533 course, the instructor, Dr. Samia Khan, has diligently commented on student blog postings by affirming student thinking, offering further guidance, and posing questions for deeper inquiry. Several of Dr. Khan’s comments to my own posts were intentionally written, I believe, to spur me on to more thoroughly consider model-based learning and its purposes. Using prior knowledge and previous perceptions I attempted to ponder the use of models within instruction and teaching, yet it was not until the T-GEM lesson during Module B that I began to see more clearly the direction which Dr. Khan was gently pointing.
For interest sake, samples from Dr. Khan’s comment prompts on model-based instruction and learning are posted below:
From “Conceptualizing Misconceptions”:
Your careful comparison of the role of visual representations in fostering partial or incorrect conceptions leads one to wonder in what ways can children’s drawings contribute to understanding in math and science and our assessment of what they know?
From “Plate Tectonics: Reshaping the Ground Below Us”
I wanted to focus in on the process of modeling for this post, which lends itself nicely to the area of plate tectonics. Gobert et al. in their paper that students can engage in model-based reasoning with models, be they dynamic, runnable visual models in WISE or ones created from physical materials such as that of the plates or the Earth. For example, one of the first activities is for students to draw a model of how mountains are formed and then explain within WISE what happens to each of the layers when a mountain is formed. Students then critique peer models using prompts in WISE such as, what do you think should be added to this model that would make it better for someone who does not know geology. Peers then revised their models by examining and considering these recommendations.
The Geology Book is currently being used to support the construction of models, and I was wondering in what ways some of these model construction, reconsideration processes be fostered in some of the activities that you already have (eg. with WISE) or with hands on-materials?
From “Staying Afloat: Sink and Float Density T-GEM”
In the modification phase, asking students to design a pictorial representation (model) of the data is one way to begin to inspect their conceptual understanding. it will be interesting to see how students represent heaver objects in these pictorial models.
By investigating varied information visualizations, specifically NetLogo, further understanding of model-based instruction and learning has developed. NetLogo contains similar features to some of the instructional frameworks studied in Module B i.e. WISE/ SKI and T-GEM. These similarities offer rich inquiry opportunities for learners and include: being overseen by experts, allowing for teacher collaboration and authoring, offering exploration of micro and macro phenomena, and student modification of models to observe patterns and anomalies. Other affordances evident in NetLogo are similar to PhET as described in the study conducted by Finkelstein, Adams, Keller, Kohl, Perkins, Podolefsky and Reid (2005). Key characteristics of inquiry simulations include an emphasis on discovery rather than verification and allow for the exploration of microscopic behaviors or patterns that are not physically observable in real-life scenarios. As described by Finkelstein et al. (2005), “[a] variety of visual cues in … computer simulations make concepts visible that are otherwise invisible to students” (p.6). Students are able to make meaning of observable global activity by viewing localized patterns. Resnick and Wilensky (1998) refer to this type of modelling as an exploratory model “start[ing] with rules for the individual parts of a system, and … observ[ing] the group-wide patterns that arise from the interactions” (p. 162). Another feature described by Finkelstein et al. (2005) is the limited nature of simulations when each simulation is designed around a focused topic. This aspect of limitation is evident in NetLogo as specific models are available across a breadth of domains, including sciences {biology, physics, chemistry, social,} mathematics, computer science, and art. Interestingly, rather than inhibiting learning, the limitations tend to result in enhancing learning by minimizing distractions caused by excessive choices. Finkelstein et al. (2005) describe this enhanced productivity in the following way:
[B]ecause the system under investigation is constrained in particular ways, students are able to make progress they cannot in an unconstrained environment… Simulations provide the instructor considerably more freedom in designing and applying constraints to ensure that students’ messing about leads to productive learning. Constraints are also valuable as students mimic real scientists and mathematicians by isolating individual variables. This isolation of variables supports student understanding “by focusing attention to relevant details… [that can be] effectively applied to physical “real world” applications. (p.7)
As a distance learning teacher working with elementary students within a range of grade levels, I have concluded that NetLogo simulations are a better fit for upper level elementary learning (i.e. grades 4-7). Browsing through the model library does takes time, yet even within my own limited exploration several models were found that could effectively be incorporated into student elementary programs i.e. Biology/Autumn (Wilensky, 2005), Biology/Sunflower (Wilensky, 2003) and Mathematics/Color Fractions (Wilensky, 2005). This latter model is quite interesting as students decide upon and view a connection between fractions, decimals and visual box patterns. This model is simple enough for a grade 4 student to modify when beginning to learn how to correlate fractions and decimals through curriculum. Each NetLogo model contains a “Model Info” section which is an invaluable feature providing teachers and students with an explanation of the model, what to pay attention to when modifying, ideas for modification, and extension ideas. This “Model Info” is an asset for successful understanding and implementation.
In conclusion, NetLogo is one example of a simulation exemplifying theoretical research through a model-based learning experience. Students are provided the opportunity to explore and discover patterns determined by their choice of modifications and scaffolding is provided within the “Model Info” section to help direct students through guided inquiry. It is necessary for both teachers and students to understand the need for invested time to become familiar with the limited variables, as this is essential in building connections. Viewing phenomena in a new and meaningful way is highly probable through NetLogo and this affordance is something, that I believe, Dr. Khan’s guided inquiry was helping lead me to see.
Finkelstein, N.D., Perkins, K.K., Adams, W., Kohl, P., Podolefsky, N., & Reid, S. (2005). When learning about the real world is better done virtually: A study of substituting computer simulations for laboratory equipment. Physics Education Research,1(1), 1-8.
Holder, J. (January 12, 2017). Conceptualizing misconceptions [Web log message]. Retrieved from https://blogs.ubc.ca/stem2017/2017/01/12/conceptualizing-misconceptions/
Holder J. (February 20, 2017). Plate tectonics: Reshaping the ground below us [Web log message]. Retrieved from https://blogs.ubc.ca/stem2017/2017/02/20/plate-tectonics-reshaping-the-ground-below-us/
Holder, J. (March 3, 2017). Staying afloat: Sink and float density t-gem [Web log message]. Retrieved from https://blogs.ubc.ca/stem2017/2017/03/03/staying-afloat-sink-and-float-density-t-gem/
Resnick, M. & Wilensky, U. (1998). Diving into complexity: Developing probabilistic decentralized thinking through role-playing activities, Journal of the Learning Sciences, 7(2), 153-172. DOI: 10.1207/s15327809jls0702_1
Wilensky, U. (2005). NetLogo Autumn model. http://ccl.northwestern.edu/netlogo/models/Autumn. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
Wilensky, U. (2005). NetLogo Color Fractions model. http://ccl.northwestern.edu/netlogo/models/ColorFractions. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
Wilensky, U. (2003). NetLogo Sunflower model. http://ccl.northwestern.edu/netlogo/models/Sunflower. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.