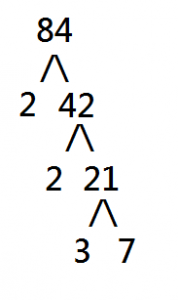Hi all.

Here’s an attempt to re-explain the factoring process.

Ex. 84

First of all, we try the branching method. Find a number which divides 84, for example, 2.
You draw a branch of 2, another branch of 84 divided by 2, which gives you 42.

And then you repeat with the remaining 42, finding a number which divides 42. And so on.
At the end of the day you should have:

Now you are ready to pick out all the factors. First you pick from the obvious, and it will be helpful if you do this in pairs.
Pulling directly from the tree:

First level: 1, 84
Second level: 2, 42
Third level: 4, 21 ( this is done by looking at the number 21, and realize that 84/21 = 4. Also, the branches that are separate from 21 is 2 and 2, which, if multiplied equals 4. )
Fourth level: 7, 12 ( again, realizing that 84/7 = 12, or take 2x2x3 )
Also on fourth level: 3, 28 ( 84/3 = 28, 7x2x2 = 28 )

We are not done. We must know that the numbers 2, 2, 3, 7 cannot be further broken down, in other words they are prime factors. ie. 2x2x3x7 = 84 That means, 2×2 is a factor, 2×3 is a factor, 2×7 is a factor, or any combination within that equation will give you a factor. So check what you missed.
2×2 = 4 ( you have that )
2×3 = 6 ( you don’t have it yet; 84/6 = 14, so 6 and 14 are factors of 84! )
2x2x3 = 12 ( you have that )
2×7 = 14 ( you have that now )

To sum it up, you have, in order from smallest to biggest:
1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84.

If this doesn’t work, try the rainbow method. This requires you to check, from smallest number up, and find a pair which multiplies to get your number. Again, using the number 84,
we know that 1×84 = 84. Next number 2 we know that 84/2 = 42, so 2 and 42 is a pair, and so on.

As you can see, both gives you the same answer, but one needs good sense of numbers, another one needs more guess and check. So pick and choose whatever you would like, as long as the answer is correct.

Some hints about finding what number divides what:
– If a number is divisible by 2, the last digit is divisible by 2.
(Ex. 32768)
– If a number is divisible by 3, the sum of all digits are divisible by 3.
(Ex. 2013 -> 2+0+1+3 = 6, which is divisible by 3, so 2013 is divisible by 3.
– If a number is divisible by 5, the last digit is divisible by 5.
(Ex. 1120, 1985)
– If a number is divisible by 11, you take (digit #1 + digit #3 + digit #5… etc), minus )digit #2 + digit #4 + digit #6… etc), and the result is 0, or is divisible by 11.
(Ex. 143 -> 1+3-4 = 0, so 143 is divisible by 11.
(Ex. 319 -> 3+9-1=11, which is divisible by 11, so 319 is divisible by 11.