I’m working with a veteran gen-ed astronomy (#astro101) instructor to make his classroom more learner-centered. We’re working hard on effective clicker implementation. The benefit of using clickers for think-pair-share (TPS) questions is the instructor can use the students’ votes to guide the instruction.
If everyone gets a question right, just confirm the answer and move on – don’t waste valuable class time re-teaching something everyone already knows! Conversely, if the students have no clue what the answer is and simply guess, you’d expect 20% for each choice A-E, 25% each if there are 4 choices, and so on. If that’s how they vote, either there’s something wrong with the question (a critical typo, perhaps) or the students haven’t learned the concept yet. Teach it again BUT NOT JUST LOUDER. Teach it again in a different way.
The “sweet spot” is when there’s a nice split between 2 or choices. The students have thought hard enough to formulate and pick the choice they feel is correct, which means they’re prepared to interact with their peers. In cases like this, we ask them to “turn to your neighbours and convince them you’re right.” Then you sit back and let them teach themselves. Ahhh.
(Well, actually, you shouldn’t sit back. You should wander around the room and eavesdrop – you’re going to hear some great ideas you can use for choices on the final exam!)
The hard part for instructors is knowing when to move on or when to get the students to discuss the question. Is 90% correct enough? Yes, probably. What about 80%? What about 60%?
In today’s astronomy class, the instructor asked the students a TPS question and the distribution of votes was A 0, B 0, C 67%, D 20%, E 13%. The instructor wasn’t overjoyed, but 67%? That means 2/3 of the students got it, right?
Wrong. Some knew the answer. And the rest guest. Er, guessed.
I did a little thought experiment with the instructor afterwards. “Suppose only half the students knew the answer and the rest just guessed. What vote distribution would you get?”
“Er, 50% then 10% for each choice, so a 60 and 10’s.”
“Great,” I said. “Suppose 2 of the 5 choices were obviously wrong. Then what.”
He thought for about 2 seconds. “67-17-17.” Our numbers from that today. “Oh.”
That’s right, when there are only 3 valid choice and only half the students know the answer, you still get about 67% success. And you might be tempted to move on even though half the students don’t know what you’re talking about!
That got me thinking – suppose fraction f of the students know the correct answer and the rest guess. What do the clicker vote distributions look like? I cast a spell with Excel (I’ve finally reached novice Excel spellcaster) and found these results:
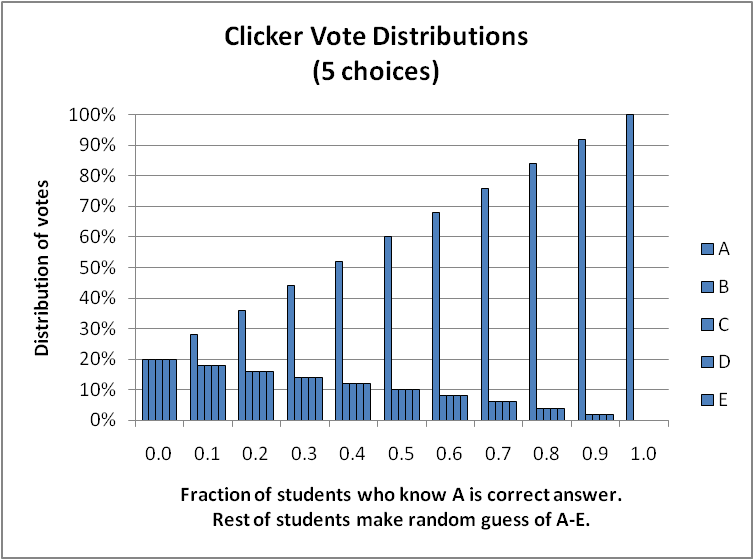
Distribution of votes when fraction f of students know the correct answer is A and the rest of the students make a random guess. Each set of 5 bars show the votes for A, B, C, D, E.
(Quick limit test that us math-types do: when no one knows and f=0.0, the votes are 20% for each choice. And when everyone knows, it’s 100-0-0-0-0. Got it.)
For example, when the peak vote is 60%, only 50% of the students actually know the answer. And it gets worse when there are fewer choices (or equivalently, when you can eliminate some of the 5 choices because they’re obviously wrong.) Here are the distributions when there are 4 choice and 3 choices:

Distribution of votes when fraction f of students know the correct answer is A and the rest of the students make a random guess. Each set of 4 bars show the votes for A, B, C, D.
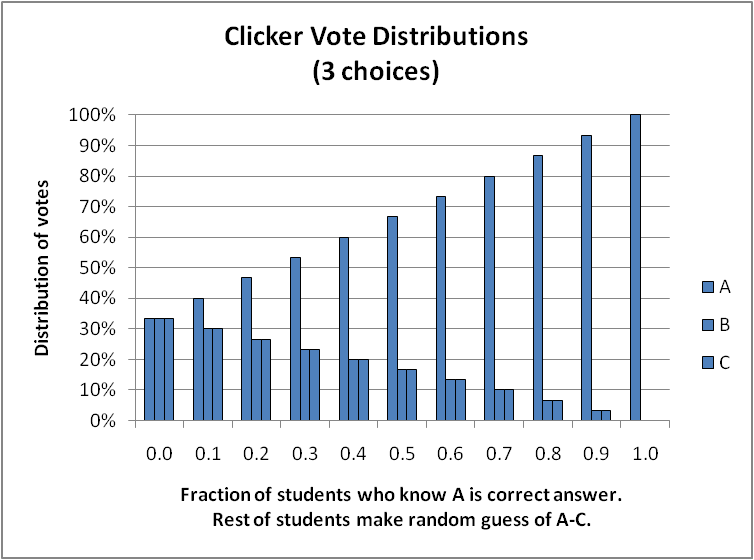
Distribution of votes when fraction f of students know the correct answer is A and the rest of the students make a random guess. Each set of 3 bars show the votes for A, B, C.
This last chart shows our 67-17-17 vote distribution corresponding to only 50% of the students knowing the right answer.
This isn’t ground-breaking research. I bet many clicker users have done this, too. Or at least, worked out a few special cases.
The moral of the story, though: the fraction of students who choose the correct answer is always higher than the fraction of students who know the correct answer. Don’t move on to the next topic unless you get a very strong peak.
What’s your threshold for moving on or doubling-back with a pair-share?


My colleague Louis just pointed out that in the 3-choices case (which many 5-choice questions reduce to after you eliminate the choices that are obviously wrong, like the one the instructor included because it’s funny) you hit 50% correct when only 25% of the students actually pick the right choice and the rest just guess. Holy run-on sentence, Batman. And holy overestimating their understanding. Raise those thresholds, people!
Pingback: Tweets that mention Clicker votes when students guess | Science Edventures -- Topsy.com
..You can have a classroom election to decide an issue that your students care about recess snacks a classroom activity… or have a mock-presidential election. ..Before beginning think of issues your students enjoy voting on make up copies of a short voter registration form for each student and have a shoe box at hand this will be the ballot box .
Pingback: So long clicker participation points « Science Learnification