I know a little bit about the differences between teaching with “blocking” or with “interleaving.” If you were teaching multiplication with blocking, you’d teach the “4 times table”, then the 5x, then the 6x and so on. With interleaving, you’d mix them up so students had to first identify what kind of question this is (“Oh, this is a 4x problem”) and then answer it. There is some nice work in cognitive psychology that shows interleaving leads to better retention.
I use the example of multiplication because that’s just what my 8-year-old was doing yesterday. He had a set of 5x flashcards that he asked me do with him. He didn’t have too much trouble, except for 5×9. As I was running through the cards, I thought of the multiplication table board I’d made a few years earlier when my other kid was learning multiplication. I remember being fascinated by a board like this when I was in Grade 3.
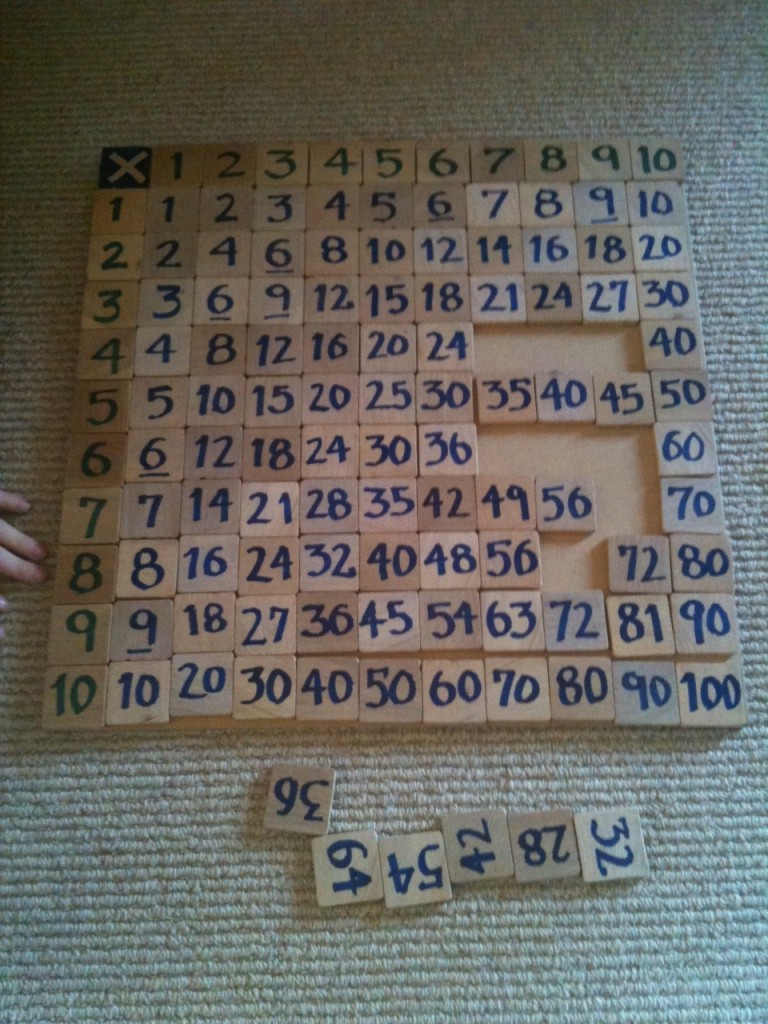
My home-made multiplication board. The green 1-10 along the top and left side are glued down. You put the 24-tile, for example, where the 4 and 6 intersect. Hmm, or the 6 and 4. Or 8 and 3 or 3 and 8!
The tiles are from a square hemlock spindle I got at the local hardware store, sliced on my mitre saw, sanded smooth, and then numbered. Green 1-10 tiles are glued across the top and down the left side. You put the blue 24-tile, for example, in the space where the 4 and 6 intersect.
My son and I got out this board, dumped the bag of tiles on the carpet, and he started to fill it in. The first row is easy: 1, 2, 3,…,10. Then he started on the second row. “2 times 1 is 2. 2 times 2 is 4. 2 time 3 is 6…” And about here, he stopped doing the multiplication and started counting by 2’s. I asked him how much 2 x 7 is, and he had to stop and think, despite the fact that he’d just placed the 10, 12, 14, and 16 tiles.
Uh-oh. My goal is to help him learn his times tables, I don’t want to reinforce repeated addition. What’ll he do with 104 x 56 next month?
So I turned the table on him. I started handing him tiles. “Here, where does this one go? How about this one?” That was pretty hard. For me, that is, because I had to quickly find the next tile I wanted in the big pile on the floor and hand it to him by the time he’d placed the current one.
I realize I was asking a different question: “What numbers multiply to give you 24?” is a lot different than, “What is 4 x 6?”. But this new version of the “game” worked nicely. He did some repeated addition in his head, searching for sequence that hit, say, 24. And he occasionally put a tile in the wrong place but I didn’t correct it. He discovered his mistakes as he lay down neighbouring tiles and the patterns were messed up. It also forced him to estimate where in the empty board to place tiles any without neighbours.
He soon discovered repeated addition works vertically, too, so he could hop down the 4-column to find the 4x tables.
After a few minutes of this, I turned it up another notch (which was possible because there were fewer tiles left in the pile and I could find them faster.) I started handing him stacks of the same tile, for example, 4 40-tiles. “Here, put these down.” I only prompted him once or twice (“Well, if 4 x 10 is 40, what about 10 x 4?”) I was astonished how quickly he picked up the symmetry. “32 goes here at 4 times 8…Oh! And over here at 8 times 4!”
Older sister dropped by to help him with the high tiles – I don’t think my son’s had much practice with the 7x, 8x, 9x tables yet. The two of them finished off the board, fighting (in that friendly brother-sister way, of course) for who gets to put in the last tile.
There are so many patterns to explore on the completed board. We discovered where on the board to find the same tile (symmetric across the diagonal) :
Me: Here’s 7 x 3 and here’s 3 x 7. Here’s 4 x 6 and here’s 6 x 4. Hey, what’s up with 5 x 5? Where’s its match?
Him: It doesn’t have one, Dad, cause 5 x 5 is the same as 5 x 5. D’uh!
A friend dropped by with a 3-year-old and she asked the toddler to his age. My son helped, helping him find all the 3-tiles. And his 8-tiles. Then my daughter (who’s 11) dropped a little nugget that confirmed this “game” was worthwhile:
Well, I don’t have a tile because my age is a prime number.
[W00t! FTW, Dad!]
I’m sure the math ed people and elementary school teachers can tell me the history of multiplication boards and best practices for using them. But it was so much fun watching my son discover the patterns for himself. And to reinforce that math is something you can play with and — Zoinks! — even have fun with!
If you’ve got the tools and some patience (100 tiles is a LOT of tiles!) I highly recommend you make a set for your kid(s). Do you have any ingenious suggestions for what to use instead of cutting wooden tiles?


Nice board! Good games! Here’s a question I like: Why is it that the numbers kitty corner to the diagonal are always one less? (ex. 4×6 is one less than 5×5) This leads very nicely into multiplication as area (how many blocks does it take to form a rectangle or a square?) Start with a 4×6 rectangle and try to reshape it into a square and see what’s missing. And later when they learn more algebra, you can ask that same question again: why is (n-1)(n+1) one less than n^2?
Thanks for the great lesson plan, Patrick. Looks like our multiplication board will in the living room for a few more years!
This is great! I’ve got an 8 yr old at home and I think he might have fun with this. I’m pretty lazy, though, so we might just start with pieces of paper.
Sharing how your kids talked about what we would call the commutative nature of multiplication reminds me of a story of my 3 yr old. He was counting cars parked on our block on a day when a neighbor was having a party. I walked along with him as he slowly counted. When we got to the end he said “let’s go back and count again!” I could tell he was genuinely interested in the result, even though he and I new there were no new cars. As we walked back and he counted I was curious to see his reaction to the fact that the number was the same no matter which way you counted it. At the last few cars he started to get excited and when he got to the end he said “hey! it’s the same”. I call this learning about the commutative nature of counting!
If I had to do it again, I’d go to 12×12. Except 2 more rows and columns add nearly 50% more tiles. I’d try to find something to buy for the tiles. And I’d make a set of addition tiles – imagine the constant “anti-diagonal” stripes! Cool.
Feltboards are the way to go if you want to avoid the woodwork but want something that can stay in place and is more durable than paper or cardboard. I have learned many great things from my childcare providing wife.
My son is 5 and I’m thinking he might like this activity as an addition board.
Great tip, Joss, thanks! I can’t count how many times I think I’ve just discovered The Next Best Thing when my wife, former K-12 teacher, tells me teachers have been doing that for eons!
Any tips on what to use to write on the felt squares? Just a Sharpie, or does the ink bleed, I wonder?
.For questions 1 and 2 the students should use multiplication to find the number of tiles in each room rather than counting by ones or equal additions. As shown on the diagram on the following page the students can find the sum of the tiles needed for rooms af by finding the area of the whole rectangle and subtracting the shaded piece 4 . .The students will need to see that the number of tiles a diagonal line passes through is the same as the number of tiles along any side…If n is even the diagonals cross 2n squares …But if n is odd one square is crossed twice so the rule is 2n 1…For example in room b which is 6 x 6 the diagonals will cross 2 x 6 12 tiles because 6 is even.
Thanks for the multiplication activity. Unfortunately, a link to the diagram you refer to didn’t make it into the comment so I’m not quite following your lesson. I’d be happy to add the diagram if you can send a url. Peter