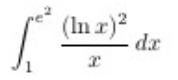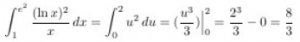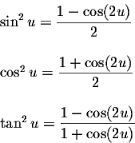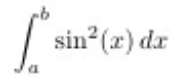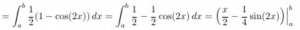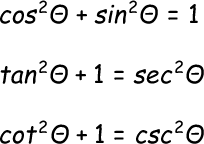The goal of using substitutions is to simplify the integral. A good substituion can solve it faster. Generally, we want to reduce the power or simplify into a ploynomial. Here are some tips on how to make a substitution in many cases.
1)
In general, we want to arrange the integral into the product of some function f(x) and its derivative f’(x). Then, f(x) would be the u-substitution.
Let u = ln x , then du = x^(-1) dx
2)
When we see trigonometric function with a power greater than 1 in the integral, such as sin(x)^2, we want to reduece the power by using the double-angle identities.
3)
Trigonometric substitution is useful when we have square root of x^2 plus or minus a constant. For example: √(x²-1) , √(4-x²) …
In this case, we can use the trigonometric identities to get rid of the square root. Some commonly used identities are:
If we let x = 2sin(t) , then the square root does not involve.