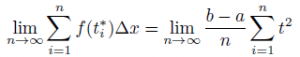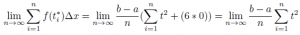Functions with finitely many removable discontinuities are integrable.
Let f(x) be a defined function on [a, b]. This function has N removable discontinuity, where N is a finite positive integer. We partition [a, b] into n subintervals of width (b-a)/n.
First, we can select all xi* to be non-discontinuous points. Second, we may select all xi* to be the discontinuous points. The area under the curve on the interval [a, b] is the same for above 2 cases.
When n is sufficiently large, the finite number N does not influence the area under the curve. Because N is too small comparing to the infinity n. No matter how big N is, it’s always possible to find a larger n.
For example, the function
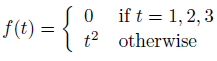has removable discontinuous at 1, 2 and 3.
If assuming partitions of [a, b] into n subintervals of equal width (b-a)/n.
When ti* ≠ 1, 2, or 3,
When ti* = 1, 2, and 3, there exists at most 6 subintervals that it is possible to choose a sample point ti* at discontinuous points.
Hence 
Therefore, functions with finitely many removable discontinuities are integrable.
——–
math 101 Assignment 1 Q3