Antidifferentiation is also known as indefinite integration. It let us find a kind of function that is another kind of function’s antiderivative. In another word, antidifferentiation is the inverse of differential that produces a formula. For example, let [F(X)+C]’=f(x), the function [F(X)+C] is a series of functions that represents antidifferentiation of the function f(x). We can find a lot of constants C to get different functions of F(X)+C. These functions we get will have the same slope, but the values of x from the various function will be different.

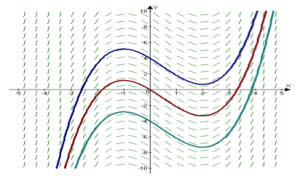
The example of anti-differentiation: let f(x)=x, then the anti-differentiation of f(x) will be F(x)= +c. (The graph shows examples of the functions F(X)+C.)

Integration is a way to calculate the sum. In integration, we calculate the total area under the curve by separating the pattern under the curve into many rectangles. When we calculate the area under the curve, we will need the interval of x which is the total width of rectangles. We can finally get a value of a function by integration

.

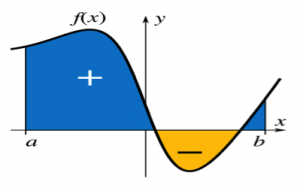
As we can see from the graph above, if we want to calculate the sum area under the curve between a and b, we can find the antiderivative of f(x) firstly, we suppose the antiderivative function is F(x)+C, and then the total area will be F(a)+C-[F(b)+C], and then, we can get an exact value.

Antidifferentiation is different from integration. As we can see, we can get a particular value by integration, and we can get a series of functions by antidifferentiation. At the same time, anti-differentiation and integration are related. We need to use the function we get through anti-differentiation to calculate integration. The constant C will be canceled when we do the calculation. Therefore, we can also consider that antidifferentiation is a step of integration.

The similar ways to change the original function that might cause students commonly mistake one from the other. Both anti-differentiation and integration make people change the original function into another function or particular value in which are related to each other.

The motivation of integration.

Welcome to the new, fantastic and marvelous field of integration.! In this section, you will be able to learn about how to use integration to solve problems in our lives.

Firstly, let’s move on to the history of the development of this mathematical concept. Over 2000 years ago, the way to calculate surface area and volume was found by a mathematician Archimedes. However, the method Archimedes found was not impeccable. For example, this algorithm can only solve simple geometric solids’ areas or volumes, such as a sphere, instead of irregular patterns, such as arches. In the 1600s, Gottfried Wilhelm Leibniz and Isaac Newton found calculus in which the fundamental idea was differentiation and integration could undo each other. This mathematical concept solves many problems in mathematics, astronomy, and physics. In 1700s-1900s, the development of integration was fast. Joseph Fourier, one of the great mathematician，found series about integration which can be used in many fields nowadays. Moreover, after Carl Friedrich Gauss, known as the Prince of Mathematics, first drawn the table of integration, then more people noticed the importance of integration and got interested in this concept. Many mathematicians such as Cauchy, Riemann and Lebesgue made a lot of contributions in developing integration. Finally, integration was published on Mathematica in 1988 and accepted widely. Obviously, integration is not only a mathematical concept but also a great treasure of human history. After learning about the history of integration, let’s move on to its practicability. Integration was applied in many fields of our life besides math. In the area of the economy, integration can be used to calculate many problems such as the best profit and the lowest cost. After that, people can find the most efficient ways of production and management that can improve the development of economy all over the world. In physics, integration is used to solve both common questions such as velocity and complex problems such as the distance between two planets. The application of integration in physics field can help people explore the unknown phenomenon. For example, the gravity was found by many calculations by scientists. Moreover, most of the concepts in physics can be inferred by using integration and differentiation such as the transformation between acceleration and velocity. In the future, some of us might be able to discover the truth of universe by using integration. In chemistry engineering, integration is used to determine the electrons and reactions, which is related to kinds of materials in our life. Frequently, integration is used in many of field observations. Researchers like to apply integration when calculating the data of regions, such as their areas and volumes.

Therefore, integration plays an important role all over the world. We are strongly encouraged to learn about this concept and apply it in kinds of fields of our lives.