Ranking
Ranking | Calculations (Arithmetic; Geometric)

For this project, a scale of 1 (least sensitive) to 5 (most sensitive) was used. The use of a standardized scale allows for the normalization and direct comparison of different variables that are quantified in different units, and permits the combination of these variables into a single index. (Gornitz 1990).

Ranking tends to be subjective, but the ranking system of Cooper and McLaughlin (2010) was adapted for the datasets available for Vancouver Island. Ranks were assigned either according to existing categories (the Roads dataset was already categorized into five distinct road classes), or by logical, natural divisions (three dominant rock types exist for bedrock lithology with known variations in strength – these were assigned the ranks 1, 3 and 5 in terms of descending rock strength). Attempts were made to keep the logic behind the ranking consistent between variables, but this is subject to error on the author’s part.

Calculations
Ranking | Calculations (Arithmetic; Geometric)

In this study, two primary sub-indexes were used: a physical index of coastal characteristics, and a socio-economical index. The two sub-indexes were combined according to the equations below to construct a final coastal sensitivity index of Vancouver Island. The arithmetic model used by Cooper and McLaughlin (2010) was chosen as the primary methodology for analysis, as the sum of variables has been shown to be less sensitive than a model that utilises the product (Gornitz and White 1992).

The algorithm used for the combination of variables can drastically affect the results of an analysis (Gornitz and White 1992). To account and quantify these differences, a geometric model (InVEST) was also applied to the datasets of interest. The results of both arithmetic and geometric models were normalized to a scale of 0-100 to allow for comparisons between the two, and the geometric model used to quantify the sensitivity of the arithmetic algorithm. (See Discussion for greater detail of the sensitivity analyses performed.)

Arithmetic
Ranking | Calculations (Arithmetic; Geometric)

The derivation of the indexes for coastal sensitivity followed Cooper and McLaughlin’s methodology, wherein they perform an arithmetic sum and normalization as a percentage of the total range using the following equations:

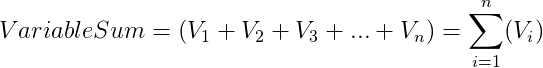
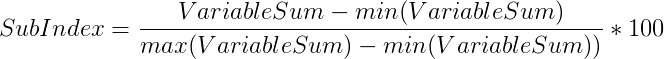
where Vi represents the variables in question. The rasters generated in the construction of the sub-indexes for this project were first combined with an equal-weight sum overlay, then normalized with the equation above using the Raster Calculator tool.

Following the construction of the sub-indexes in Cooper and McLaughlin’s work, the generation of the final coastal sensitivity index could be performed by the merging of the sub-indexes by an arithmetic mean:

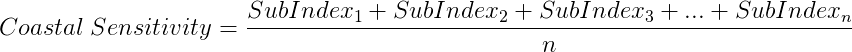
Geometric
Ranking | Calculations (Arithmetic; Geometric)

The derivation of the sub-indexes used in this algorithm was based on the calculations used in the InVEST Coastal Vulnerability Model, which proceeds as follows: