In February 2018, The World Health Organization (WHO) updated their list of priority diseases to research—diseases that most likely to lead to a global pandemic, including infamous diseases like Ebola (Figure 1), Middle East respiratory syndrome, and Zika. However, there’s one disease confusing many people, with the ominous name “Disease X”. Just what is this mysterious disease?
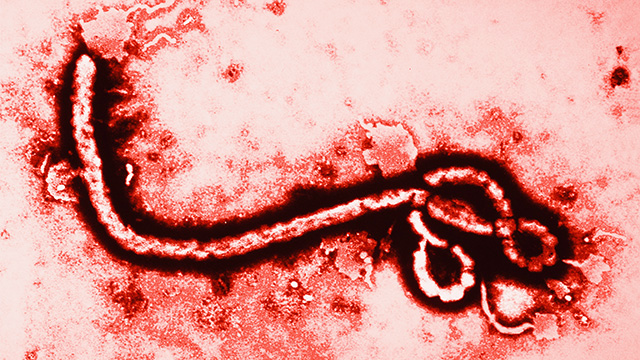
Figure 1: The Ebola virus magnified 108,000 times. Source: ARS Technica.
It turns out Disease X is the name given for an unknown disease, i.e. the WHO thinks it is likely a pathogen that we do not yet know about could cause the greatest devastation to humanity; this makes sense—if we don’t know how to respond to something, it would be probably have a dire impact.
But imagine this: we now know Disease X is a terrifying disease, with only mild symptoms the first few days, but is quickly followed by much more unpleasant symptoms and death, partially because we don’t know how to deal with it yet. We also know it’s a relatively rare disease.
Say you live in a village of 100 people, and the village’s water supply was infected so that anyone in the village has a 1% chance of contracting the disease. You don’t feel very well, so you take a test correctly identifying 95% of people with the disease. You then get the test, which identifies you as having the disease. At this point, you would probably be quite worried. How certain is it that you have the disease? You might think there’s a 95% chance—but fear not—it’s much lower than that! This is where Bayes’ Theorem (Figure 2) comes in handy.
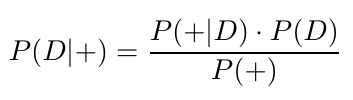
Figure 2: Bayes’ Theorem (tailored for our example)
D represents you contracting the disease, and + represents being tested positive by the exam. P(D|+) would then be the probability of testing positive if you had the disease, P(+) the probability of having the disease, and the probability of a positive test (which consists of testing positive given that you have the disease, and testing positive when you don’t, i.e. a false positive). Plugging in these numbers, it turns out there is only a 16% chance of having the disease if you test positive!
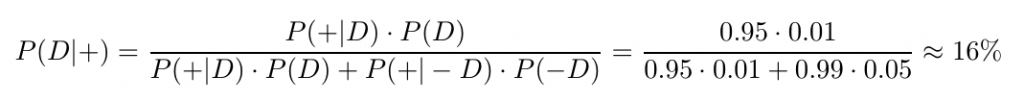
This seems counterintuitive, but think about this: the test would likely identify someone with the disease, but also incorrectly identify 5% of the population as having the disease (Figures 3-4).
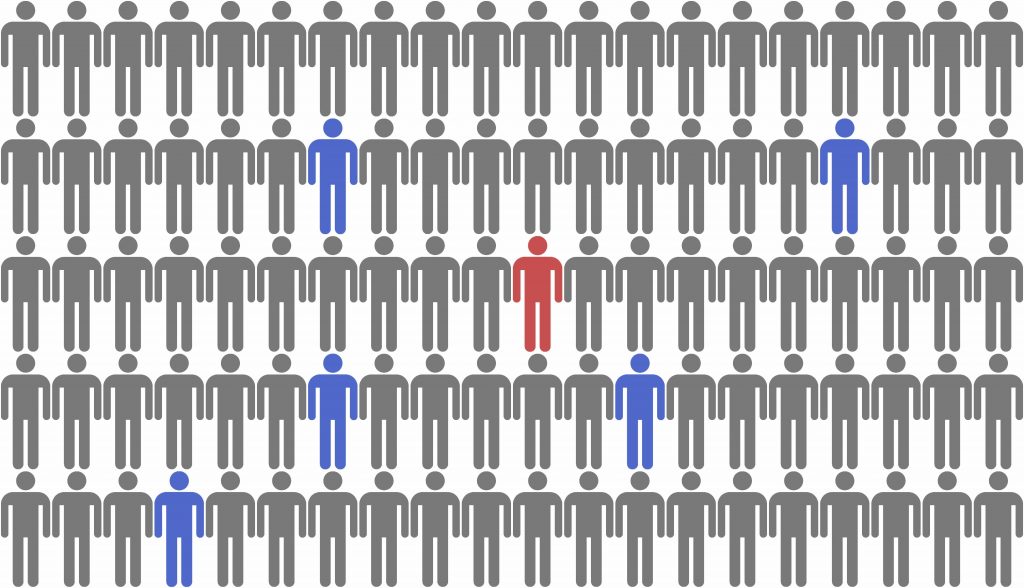
Figure 3: In a population of 100, 1 person will have the disease, while 5 people will be falsely identified. Graphic obtained from clker.com.

Figure 4: Your chances of having the disease are 1 in 6, or 16%. Graphic obtained from clker.com.
So if the test on average identifies 6 people as having the disease, how certain can we be that they actually all have the disease? That number would be 16% of 16% of 16%… six times: 0.002%, or basically zero.
In reality, most tests are less accurate than 95%. For example, a mammogram has a 18% chance of a false positive of breast cancer in healthy women.
Bayes’ Theorem has many applications in fields such as epidemiology (the study of the distribution of health and disease) and computer science. It’s so powerful, in fact, that this way of thinking has been given a name: Bayesian logic. So the next time you’re absolutely certain of something, you might want to think twice.
-Cliff Ng
