Dating and settle down are big problems for a lot of people, especially for many scientists, who spend their entire life in labs. For rich people, dating can be easily solved by economics. However, for the poor, dating is a metaphysics problem. How can we dating and settle down efficiently? It turns out that there are many mathematical rules that tell you how long you ought to search, and when you should stop searching and settle down.
Secretary problem
The secretary problem is a problem that demonstrates a scenario involving optimal stopping theory. In the secretary problem, an administrator is interviewing n applicants in turn to help the company to hire a best secretary. A decision must be made immediately after each interview, and once the interviewee has been rejected, it cannot be recalled. The question is about the optimal strategy to maximize the probability of selecting the best applicant.
Similarly, for dating and marriage, you must decide whether to settle down with your current boyfriend or girlfriend at some time points. This can be solved by the secretary problem. For example, assuming you have 3 different boyfriends in your lifetime, and you need to choose one to marry him. The best strategy for you is to break up with your first boyfriend regardless of how excellent he is, try the second one. If the second one is better than the first one, marry him, or try the third one. In this case, you have ½ probability to choose the best guy, which is more probable than choosing randomly.
Demonstration on the scenario talked above.
The 37% Rule
However, in the real life. The sample size is unpredictable, and largely depends on a lot of things. How large the sample size should be and how many boyfriends should you “try” before you make the decision?
First, we can make an assumption: There are n boys chasing you, you try first k (k<n) boys but reject all of them. From the k+1 boy, settling down if he is better than the previous ones. For example, when n=4, there’re 4 possible k values: k=0, 1, 2, 3. By listing all possible cases, we got when k=1, P(1)=11/24, which is the best strategy for you to choose the “Mr. Right”.
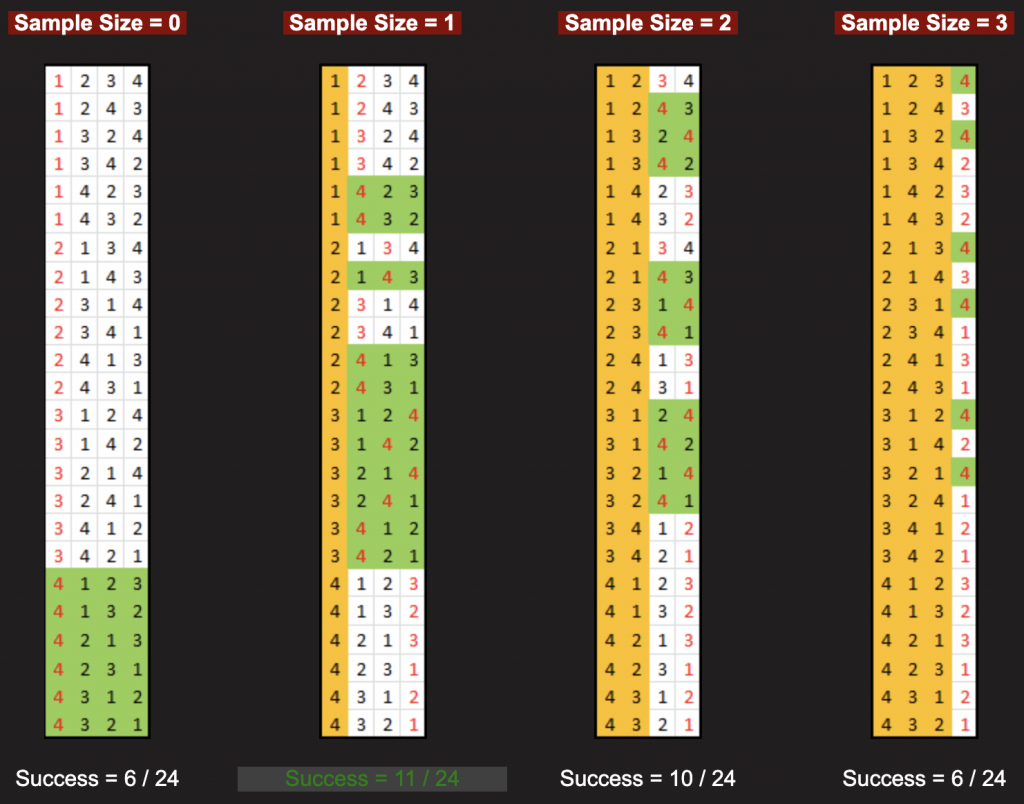
Possible cases for Sample size=4. (Source: DataGenentics)
More generally, for a very large sample size, the probability can be calculated from Riemann integral and its derivative:
Which means you should settle down immediately when you meet the “best boy” after you try first 36.8% guys in your life.
Comparing with choosing randomly, it is obvious that when the sample size is larger than 2, using The 37% Rule is much more possible to settle down with your “Mr. Right”.
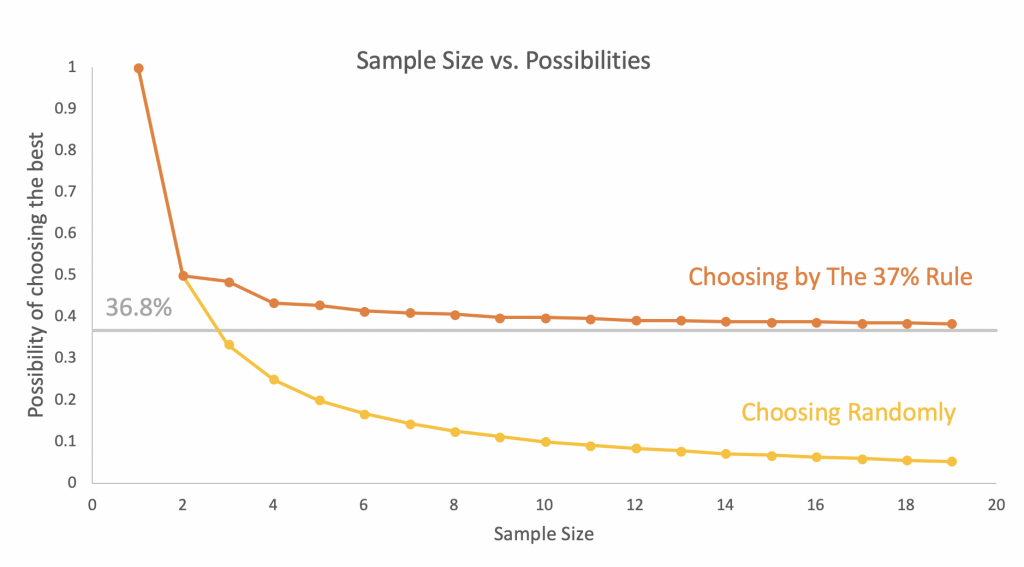
A comparison of choosing randomly and choosing by the 37% rule. (Data Source: DataGenentics)
However, in the real world, you never know how large the sample size is. Although we can approximate a n value by combining many factors like economic status, educations, personal experiences, family background, face score and etc. Life is not a game, so settle down in a relationship with your true love when you think he or she is your best choice.
3 responses to “Strategic Dating: The 37% Rule”