The Crow and the Pitcher
The Crow and the Pitcher is one of Aesop’s Fables, which tells a story of: A thirsty Crow found a high and narrow-neck pitcher with a little water in it, the crow could not reach the water no matter how it tried. Suddenly, the crow came up with an idea: picking up some small rocks and dropping them to the pitcher. With each pebble, the water rose higher and higher. Finally, the crow drank the water.

The Crow and the Pitcher, Aesop’s Fables. (Copyright: Milo Winter)
This story is very inspiring to many children, it told them to think flexibly when facing problems. However, is it possible for the crow to drink the water with rocks in real life?
Close Packing of Equal Spheres
The problem in the Crow and the Pitcher is that after the crow dropped rocks to the flask, the water filled the space between rocks first, then it raised the height of water. How much water was needed to fill the space between rocks, this is the closest packing problem.
The Close Packing of Equal Spheres was first put forwarded by Kepler in the 17th-century. Kepler thought that the close packing of equal spheres in a three-dimensional space looks like the following:
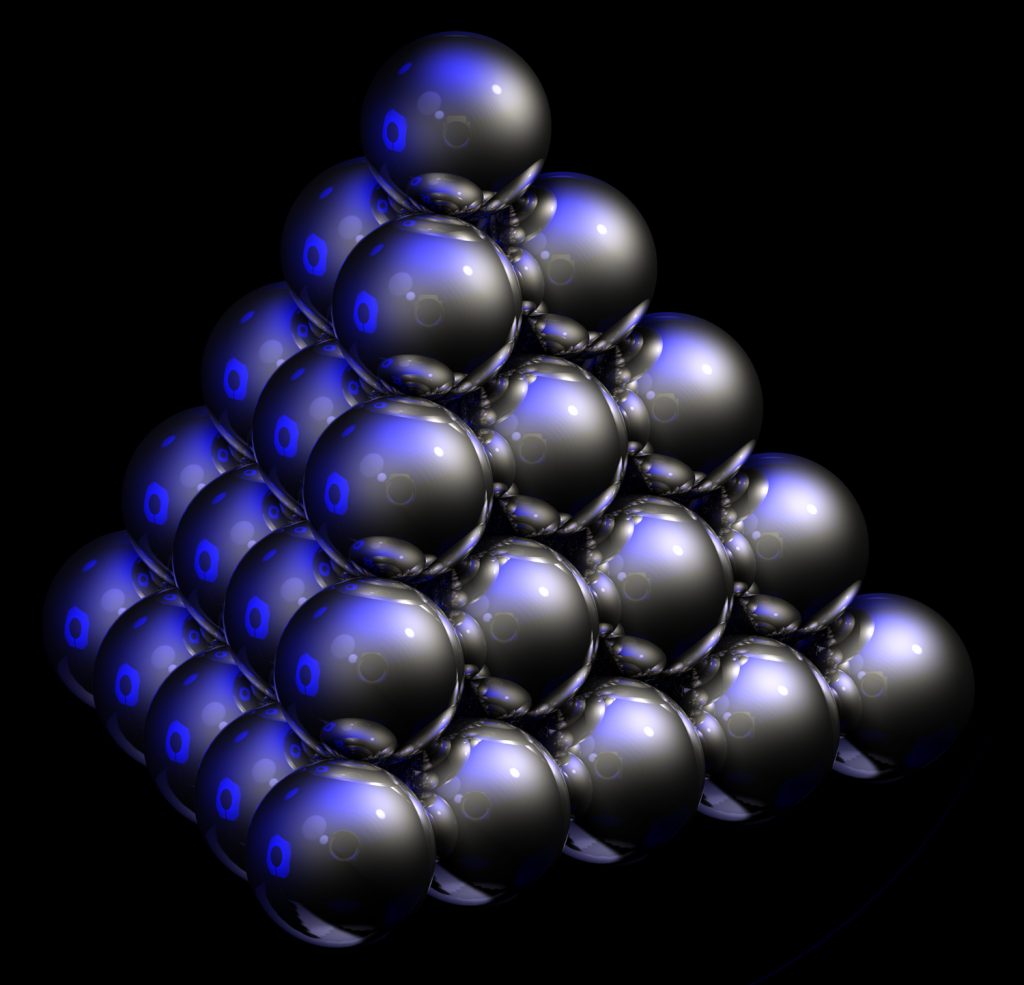
The cannonball stack: an “FCC” latice. (Copyright: Wikipedia)
The close packing of equal spheres can be widely found in chemistry, such as crystal structures of Magnesium and Copper atoms. It was calculated by Carl Friedrich Gauss that the greatest fraction of space occupied by spheres – that can be achieved by close packing of equal spheres is 74%. In other words, if the water in the pitcher is 26% (volume) or less, the crow cannot drink the water no matter how many rocks it put in the pitcher.
The close packing of equal spheres also called the Hexagonal Close Packing. In 2017, the scientist proved that the Hexagonal Close Packing is the densest arrangement in the three-dimensional space.
How can the crow drink the water in the pitcher?
Is there a way that the crow can drink the water in the pitcher without 26% of water? Mathematicians said that by combining the truncated octahedrons, tetrahedrons and octahedrons (2:1), or truncated cubes and octahedrons (1:1), or gossip mirrors and truncated cuboctahedrons (3:1), the crow can easily drink all the water in the pitcher.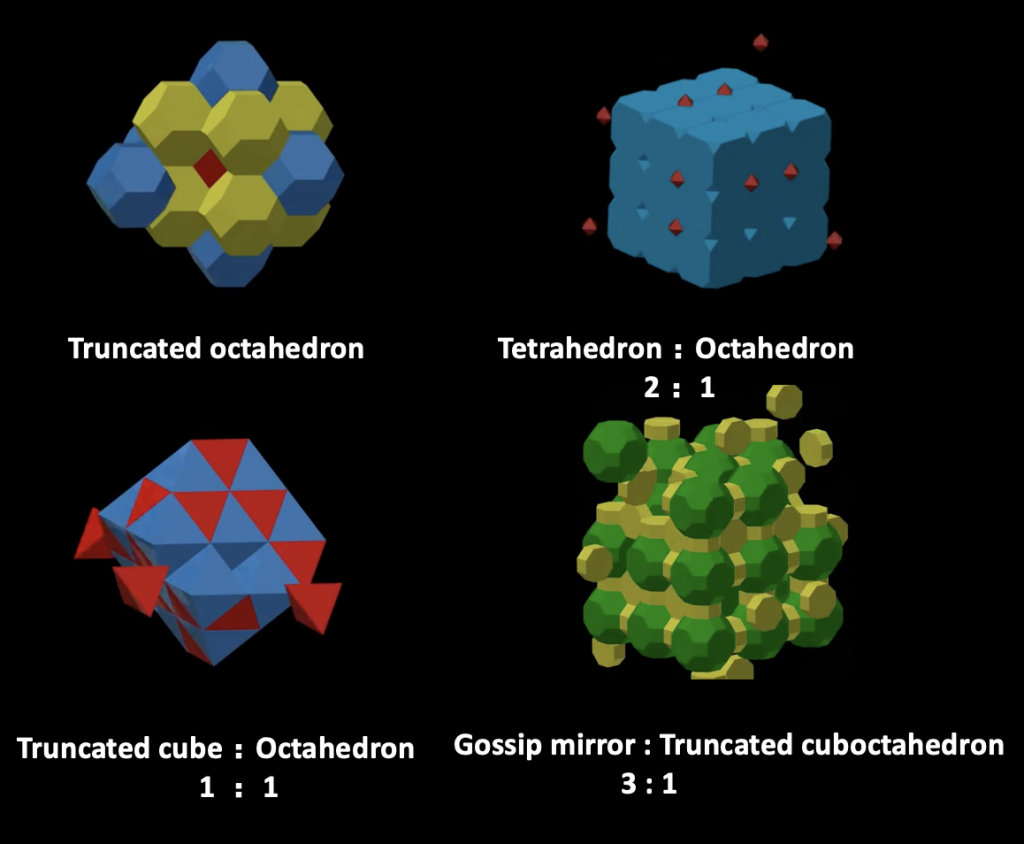
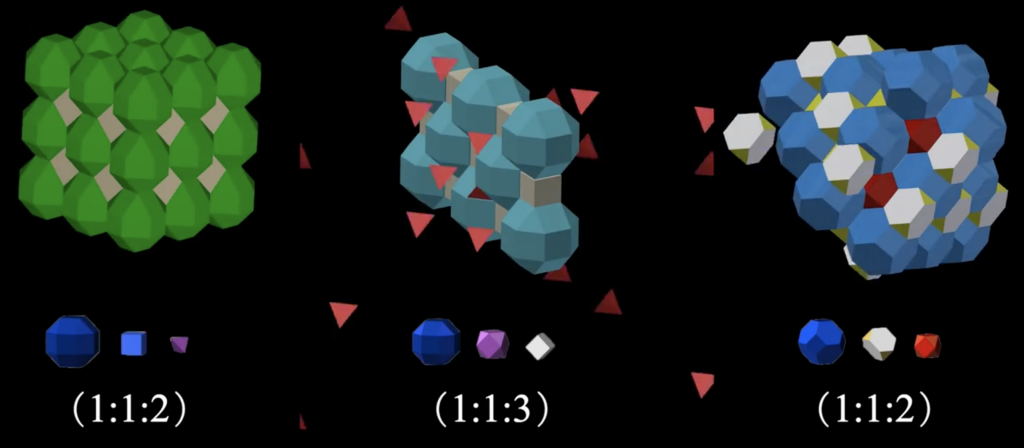
Alternative ways for the crow to drink water in the pitcher. (Copyright: ScienceDirect)
If it is hard for the crow to find the above rocks, it can also combine multiple shapes of rocks to get the water in the pitcher. Moreover, some scientists tested the effect of shapes of flasks on the increasing heights of water in flasks by using the Close packing of equal spheres. They found that the height of water in Erlenmeyer-flask-shaped flasks has the fastest increase. However, where can you find an Erlenmeyer flask? -A chemistry lab. It’s absolutely a bad idea to drink solutions in a chemistry lab.
