Introduction
This assignment is to explain a relatively complex term related to my profession to readers that do not have professional knowledge in the field. The goal is to make a clear and easy explanation for non-professional readers. I will explain a term in the software engineering field to the relevant departments working together who are not familiar with software engineering but willing to know about the basic knowledge on software engineering. As the expected readers do not have technical knowledge in the software engineering field, I will try to explain the term as understandable as possible.
Parenthetical Definition
Recursion(repeating the same function for the compound data type) is used for software development when dealing with data that has a sequence.
Sentence Definition
Recursion is a way of solving a problem in computer programming, by creating a function that repeats itself inside the function. (University of Utah, n.d.) This way of programming is usually used when a same process is applied to multiple elements of a single kind of data.
Expanded Definition
History
Recursion is not originated from computer scientists. The method can be found even in ancient ages in the mathematics field. One of the most famous mathematicians who used recursion was Leonardo of Pisa, who introduced a sequence of numbers called Fibonacci numbers. The methodology was adopted to this field by the initial generation of computer scientists, who were extremely familiar with mathematics. (Stanford University, 2020)
Example
Here I will show the example. This is a function for adding up all the numbers in a given list of numbers.
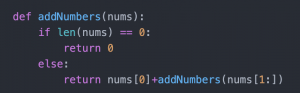
If I run the example function and put a list containing 1, 2, 3, the process is as below:
addNumbers([1,2,3])
As the length of [1,2,3] is not 0, return 1 + addNumbers([2,3])
As the length of [2,3] is not 0, return 2 + addNumbers([3]). The whole process is now 1+2+addNumbers([3]).
As the length of [3] is not 0, return 3+addNumbers(empty list). The whole process is now 1+2+3+addNumbers(empty list).
As the length of an empty list is 0, return 0. The whole process is now 1+2+3+0. There is no more function left, so the result is 1+2+3+0, which is 6.
In the example, you can see that there is a name of a function and the contents, but the name of the function appears again in the function. This is how recursion works. By dividing the given list into two parts, the first element and the rest part of the list, you can deal with the first element and do the same operation to the rest part of the list by putting the rest part into the same function, just as I added the first element to the result of the same function that was given the rest part of the list.
Analysis of Parts
As you can also see in the example, recursion code can be divided into three parts: base case, operation for the first element, and recursive call. First, you define the base case. It means you need to set when to stop repeating the function. Next, you choose what to do with the first element. In the example above, I did nothing with the first element but just adding to the next recursion, but you can deal with it in other ways, such as other math operations, adding words, or checking whether it is the element that I need. Finally, in the recursive call step, you write the function again whose given data is the rest part of the list. Then, you can easily find that the recursion works.
Required Conditions
Recursion is a useful methodology in software development especially when you are dealing with complex data that contains multiple elements and you feel it is hard to deal with the whole data. By using recursion, you can separate the data into pieces and concentrate only on a small piece of the data. However, to use recursion, you need some conditions. First, of course, the data must be in sequence. For example, it can be compound data such as list. Otherwise, it should have the next sequences, such as a number that can go to the next sequence by subtracted or added, or words that can go to the next character. Also, if you are willing to make an efficient program, using recursion is not always the best choice. Sometimes, especially when the data is very large, it is very efficient because calling a function repeatedly consumes larger memory and more data than just dealing with it by one function. If there are customers’ complaints that the process of our program is too slow, maybe inappropriate recursion can be one option to check.
Reference
Stanford University. (2020, April 23). Recursive Functions (Stanford Encyclopedia of Philosophy). Stanford Encyclopedia of Philosophy. Retrieved January 30, 2022, from https://plato.stanford.edu/entries/recursive-functions/
University of Utah. (n.d.). Programming – Recursion. Jim’s Computer Science Topics Area. Retrieved January 30, 2022, from https://www.cs.utah.edu/%7Egermain/PPS/Topics/recursion.html
Leave a Reply