The Definitions of a “Binary Search Tree”

This post describes a parenthetical, sentence, and an expanded definition of relatively complex term . This post has the following objectives:

• Appreciate the importance and role of definitions in technical writing
• Understand how audience and purpose indicate the need for definition
• Differentiate between the levels of details in the definition
• Select the right level of detail according to the situation

In this post, we will be describing the term Binary Search Tree (BST) in the aforementioned ways.

The Situation

The situation is a professor describing the term Binary Search Tree to a one of their students.

Parenthetical Definition

A Binary Search Tree (BST), is a rooted binary tree data structure whose nodes each store a key greater than all the keys in the node’s left subtree and less than those in its right subtree.

Sentence Definition

A Binary Search Tree is a node-based binary tree data structure. It is a data structure that ensures each node only contains smaller values than its key in the subtree to its left, and larger values than its key in the subtree to the right.

Expanded Definition

Analysis of Parts

The term “Binary Search Tree” is a composition of simpler parts:

1. Node – A placeholder for two pieces of data. Each node has a “name”, known as a key, and a value. The value could store many things, such as a number, some text, or another node
2. Tree Data Structure – A non-linear data structure consisting of nodes. In this structure, each node contains one or many other nodes as its value(s).
3. Binary Tree – A binary tree is a tree where each node can have at most two children

Finally, a binary tree can be considered a Binary Search Tree if each node’s left child contains key values smaller than its own, and each node’s right child contains a value larger than its own. This condition must hold for all of the nodes in a tree.

Comparison & Contrast

Data structures are primarily evaluated by their performance in one metric – how quickly they can perform a set of operations. These operations include

• Adding an element
• Removing an element
• Searching for a given element

Consider a simple data structure such as an Array. Unlike a binary search tree, an array can be thought of as storing all of its elements beside eachother. Compared to an array, a binary search tree has the following advantages:

• Faster at “finding” a particular element
• Faster at deleting a particualr element
• Faster at finding the minimum and maximum values

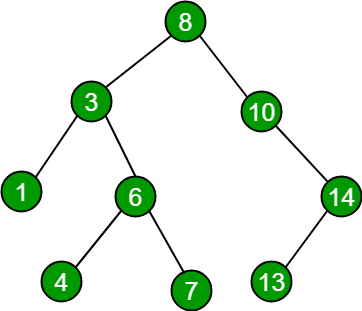
Visuals & Examples

The following image shows two trees. The left tree is a Binary Search Tree, while the right tree cannot be considered a binary search tree. Returning to our definition, we can notice that the node containing the key “2”, highlighted in red, is to the right of the node containing the key “3”. This violates the rules describing a binary search tree.

References

“Binary Search Tree.” Wikipedia, Wikimedia Foundation, 30 Jan. 2022, https://en.wikipedia.org/wiki/Binary_search_tree.

“Binary Search Tree.” GeeksforGeeks, https://www.geeksforgeeks.org/binary-search-tree-data-structure/

“Tree Data Structure.” Programiz, https://www.programiz.com/dsa/trees.

“Check If given Sorted Sub-Sequence Exists in Binary Search Tree.” GeeksforGeeks, 4 July 2021, https://www.geeksforgeeks.org/check-if-given-sorted-sub-sequence-exists-in-binary-search-tree/.