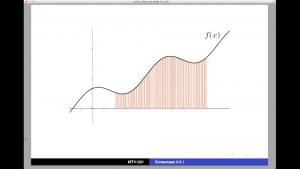
Students always think that integration is the same as antidifferentiation. Let us define these two terms now
Integration is a number associated with a function, what is usually called a “definite integral.” It is defined by a limiting process which means in a certain range or on a domain. That is what we have already learned, Riemann sum, in the class.
For “Riemann sums” by separate the domain equally into n rectangles and approximating the area under the function graph by adding those rectangles together, which are in the subinterval.
So, we can describe integration which is “definite integral” by this expression:
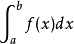
An antiderivative of f is a function whose derivative is f. Thus, if F is
an antiderivative of f, then F’= f. In another way, antidifferentiation is the reverse process of differentiation.
Antidifferentiation not focus on certain interval but work on the whole function. For example, f'(x) = 2x, then we know that the antiderivative of this function is f(x) = x^2.
We can define the antidifferentiation which is “indefinite integral” by this expression:
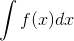
All in all, “Antidifferentiation” math circle is within “Integration” math circle. When we calculate integration we need to use the method of antidifferentiation.
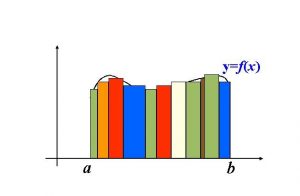 like these rectangles
like these rectangles