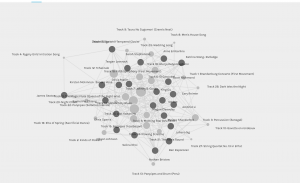
Golden Record Curation Network generated by Palladio for ETEC 540

To be honest, I don’t have a strong understanding of algorithms and the terminology that I use in this reflection may make that quite obvious, but please bear with me. I do understand algorithms to be a set of instructions that help solve problems, but I wonder what problem is being solved with the Palladio program. When I look at the whole class graph/network it all seems pretty straight forward, the program has shown the connectivity of the class and their respective song choices for task 8. I could draw something like this by hand fairly easily by drawing a node for each song and each person, and then connecting them with a line. There wouldn’t be a need, necessarily, for any math in order for me to do this. Similarly, if I play around with the data and force groups of people, say for example forcing a grouping between Meipsy, Nathan, and Allison, I can see their connectivity and understand exactly how Palladio generated that graph.

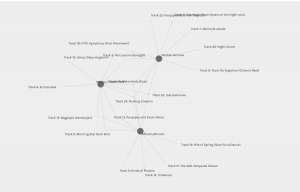
Forced network grouping of Meipsy, Nathan, and Allsion

However, I wonder what set of instructions Palladio is using to group the members of each class. I would suspect it’s optimizing the in-group connectivity, but I’m not sure. Why does it put students into groups of 3 or 4? Why not two groups of 8 and one group of 7? Or why not groups of 4 or 5? Is this a default setting, is it part of the optimization, or was this predetermined by our instructor? 

The groupings generated by Palladio grouped James, Nathan, and myself together. As you can see in the image below, we have a high degree of connectivity with each other (with James and I being slightly more connected in the grouping than Nathan).

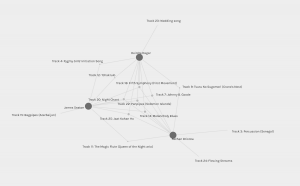
Palladio generated network grouping of Nathan, James, and Deirdre

Nathan has a good write up in his reflection about why he suspects we had such similar song choices. I don’t necessarily want to duplicate what he’s written, but I do agree that part of the reason is because the three of us created similar constraints for our song choices. Other similarities we share (those that I could glean from the info hidden in our blog posts) include the fact that we’re all high school teachers in math and science, and I’m assuming, generationally we’re all millennials. Though there are other people in our class who fall into those demographics (e.g. Ying)  and their song choices were not similar enough to be grouped with us. I suspect the constraints we determined for our song choices is a better reflection of grouping than anything about us demographically. But then again, maybe our demographics affected the constraints we decided on. Interestingly, Nathan and I actually know of each other having worked in the same remote region of Canada. Is there a shared personality trait that would lead us to both work in the Arctic and teach math and science and come up with the same choices of songs? I wonder how many other small world connections there might be in the other groupings. 

Had Nathan, James, or myself just chosen what we personally liked, would we have still ended up in the same group? 

Curiously, Palladio excluded Katrina from our group despite the fact that she shared 7 song choices with myself, 7 songs with James, and 6 with Nathan. I’ve included images of Katrina grouped according to Palladio and then grouped with my grouping.

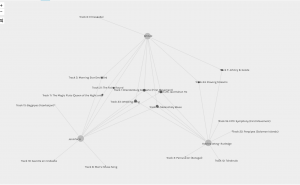
Katrina’s original network grouping generated by Palladio

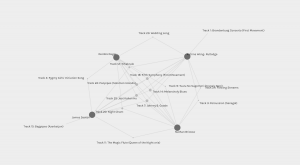
Katrina grouped with Nathan, James, and Deirdre

Interestingly, when visiting Katrina’s blogpost, she had similar constraints for herself when it came to song choices. Why then, did Palladio’s algorithm parse the data the way it did?

Another area of exploration is looking at who I shared the least amount of song choices with. In this case, Ben and myself only shared 2 song choices. I can’t speculate on why, given that I don’t have access to Ben’s reflections, but if my hypothesis is right, I would suspect that with respect to song choices, Ben had constraints that differed from mine.

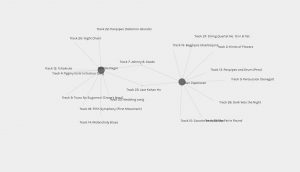
Network depicting the connections between myself, Ben, and our song choices

One last thing I am curious about is if there are any two people in our class whose song choices excluded each other. I wasn’t able to determine an easy way to manipulate the information in Palladio in order to see that without manually examining each pairing of students.

Essentially, the issue at hand is whether or not Palladio’s groupings can accurately reflect anything more than just the network of connections of song choices, and the strength of the choices. Perhaps it would be helpful to have some insights into the biases or instructions used by the Palladio algorithm. Otherwise, I’m not convinced that a network like this can tell us anything about “why.” Why did our class overwhelmingly choose Johnny B. Goode and so few of us chose Men’s House Song?