For my post about Information Visualization, I will be combining information visualization with the LfU laid out in Edelson (2001) in order to design a lesson that helps them explore and arrive at the proper calculation of π.

• Motivation
  • Create a story for the students about how the classroom is going to be getting new carpet (or any other story that would actually work). But, the budget is pretty tight, so we need to order the best amount of carpet. What’s more, the warehouse is offering us a special incentive: if we can guess the exact area of the carpet we are trying to buy, then we get a huge discount.
• Elicit Curiosity
  • There’s only one problem: the school board can’t approve carpet SQUARES or RECTANGLES. They can only get around the wording if we measure it using circles. (A long shot, I know, but hey, what’s written is written!)
• Observe
  • Students would first need to visualize, measure, and draw on background knowledge of areas.
  • Measuring the room would allow students to arrive at the borders of the room. Also, students would be asked to use pictures to illustrate their ideas, as Edens & Potter (2008) tell us that “an important process of the problem-solving cycle is the translation of the problem into a meaningful representation.” Students could begin doing this on paper, drawing schematics, that is, illustrations that represent proportions, not details. Think, diagrams for problem-solving.
• Communicate
  • Next, students would need to talk to each other about differing methods they have devised for measure the circle that is going to take up the middle of the room.
  • Using The Geometer’s Sketchpad, they would be able to graph and measure different polygons that fit into the circle, as shown below:
  • 
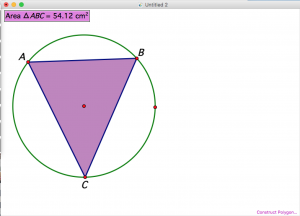
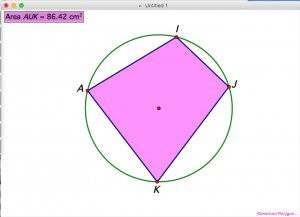
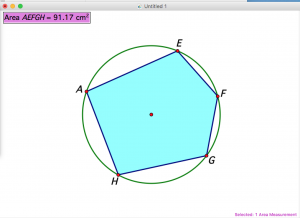
  • By using increasingly complex shapes, students would be able to explore and start to be able to deduce methods of finding the exact area of a circle.
  • This process of exploring a phenomenon and connecting it to the mechanisms is the basis for Model-Based Inquiry (MBI) as told by Xiang & Passmore (2015).
  • Throughout this process, students would be encouraged and required to explicitly communicate with each other to verbalize and denote their predictions and explanations, to further match the MBI model (Xiang & Passmore, 2015).
  • At some point, Xiang & Passmore (2015) would say that students may require further scaffolding. This could be provided in varying formats depending on how the students are progressing. For example, if students are drastically struggling, a bare-bones formula could be given to them A= ? ?^2 and allow them to fill in the blanks through more discovery. If they are progressing nicely, perhaps another way would be to instruct them to map out and figure the area of the spaces that are not taken up by the shapes as closely as they could.
  • At every point, students would be pointed back to the model being created on the Geometer’s Sketchpad, as “schematic representations are associated with successful problem solving,” (Edens & Potter, 2008).

• Reflect
  • When most groups have come up with the solution or gotten close, students would be given a chance to now verbally express and represent the knowledge that they have earned through the geometric representation of A=πr^2.
  • A chance for reflection and correction of the process that they took to arrive at the equation would further enlighten them and cement the ideas in their mind.
• Apply
  • At the very end, the equation could be used to then measure out the size of a circle that would fit in the room, or any other location that they wish to choose.
  • To extend the learning, they price per square foot of the carpet could be provided and further calculations with that data could be done to figure out how much it would cost to cover the circle or the room.

It may seem like quite the lofty goal for students to be able to arrive as the equation on their own, but with a visualization tool like the Geometer’s Sketchpad, the amount of tinkering that is easily possible is immense, therefore the potential for learning is also immense. The easy access of tools could scaffold students as they inquire, explore, and build. The ability to quickly construct multiple models and compare them would give students a chance to use further geometric knowledge and proportions to arrive at answers, all while the teacher is there as a support and fellow questioner, encouraging and spurring on further inquiry. In a worst-case scenario, a teacher could even design a model that students could then use to explore the measurements of and arrive at a deeper understanding than if they had designed the model themselves.

The combination of these different methods create a situation where both student and teacher are active, inquiring, and learning in authentic ways that are truly useful, with applications that extend far outside the classroom. Futhermore, with the technology enhancing the learning, students are not limited by their own drawing ability, a factor that was noted as a potential stumbling block to learning (Edens & Potter 2008).

Resources:

Edelson, D. C. (2001). Learning‐for‐use: A framework for the design of technology‐supported inquiry activities. Journal of Research in Science teaching, 38(3), 355-385.

Edens, K., & Potter, E. (2008). How students “unpack” the structure of a word problem: Graphic representations and problem solving. School Science and Mathematics, 108(5), 184-196.

Xiang, L., & Passmore, C. (2015). A framework for model-based inquiry through agent-based programming. Journal of Science Education and Technology, 24(2-3), 311-329.