Not included in this e-Porfolio but present in the Excel file:
Table 1: Raw data collected using stratified sampling (35×5=175 total subjects)
Statistical Analysis 1: T-test for Independent Means
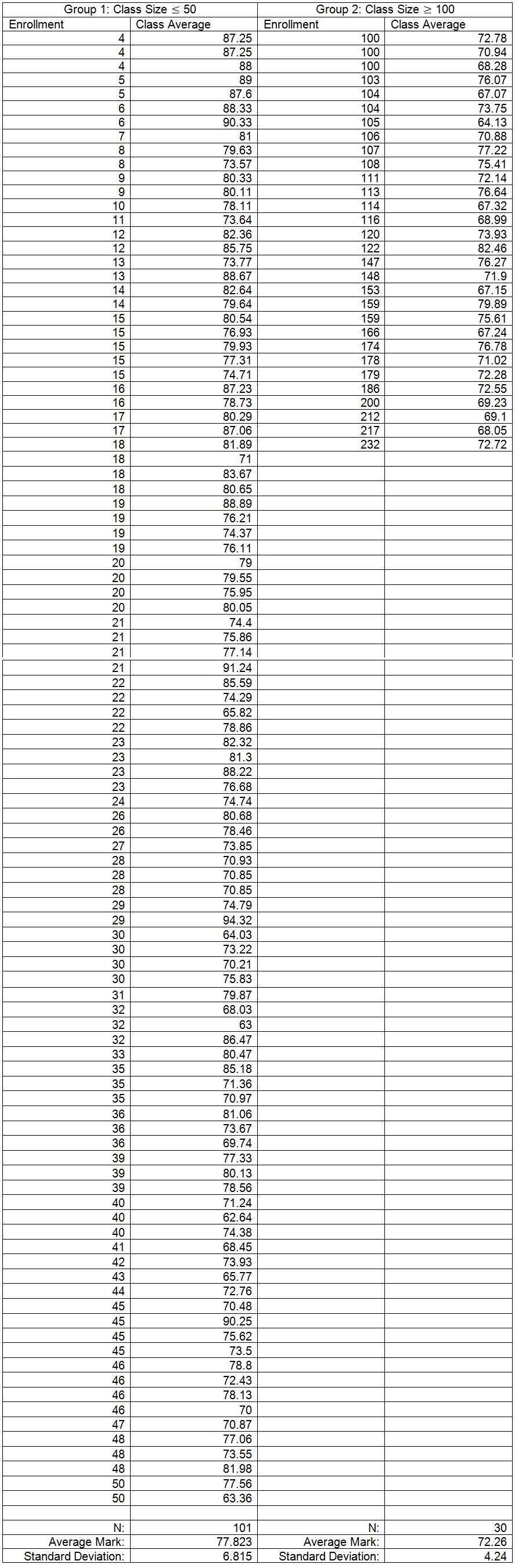
Table 2: Data for 2 independent groups of classes and their sample estimates
1. Set up hypothesis:
H0: μ1 = μ2 There is no relationship between the class size and average marks.
Ha: μ1 > μ2 Smaller classes should achieve higher averages than larger classes.
2. Choose method and significance level:
T-test; α = 5%
3. Calculate t-statistic:
SEest = (6.815^2/101 + 4.24^2/30)^0.5 = 1.029
t = (77.823 – 72.26)/1.029 = 5.406
4. Compare t-statistics vs. α
d.f. = 30 – 1 = 29
The t* multiplier that corresponds to α=0.05 and d.f.=29 is 1.699.
Because t > 1.699, we fail to reject Ha and reject H0
Statistical Analysis 2: Regression
Dependent variable: Class Average Mark
| Parameter | Estimate | Standard Error | T-Stat | P-Value |
| Intercept | 79.17 | 0.707 | 111.982 | 2.3E-163 |
| Class Size | -0.0549 | 0.0095 | -5.772 | 3.55E-08 |
Table 3: Regression statistics obtained using Excel
Hypothesis: H0: b1 = 0 Slope is zero because class size has no influence on scores.
Ha: b1 < 0 Slope is negative because bigger classes lead to lower scores.
The p-value is way smaller than our significance level of 0.05, therefore we reject H0.
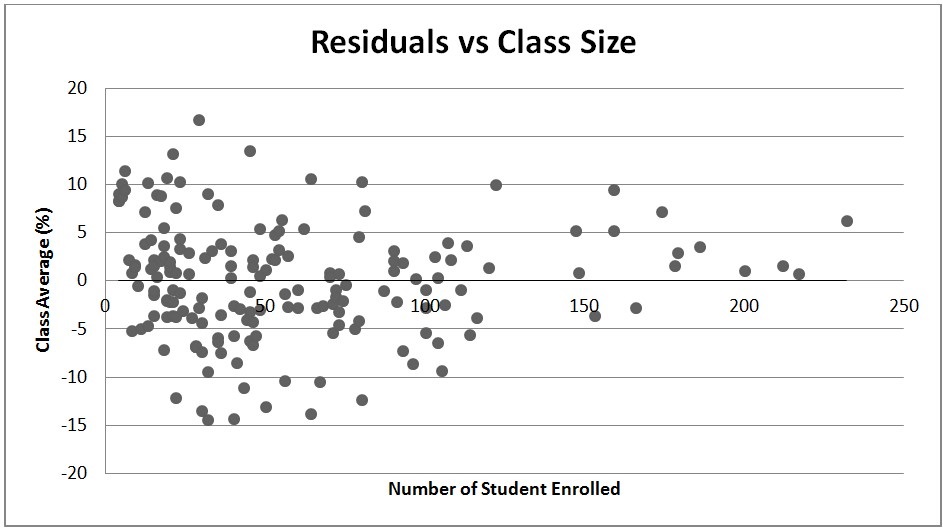
The average of the residuals calculated in Excel is -0.001.
Graph 4: Scatter plot of class average vs. class size for the entire sample
Graph 5: Scatter plot of residuals vs. class size for the entire sample
Graph 6: Scatter plots for the two groups analyzed in T-test
Graph 7: Scatter plots for select strata (academic discipline)