The distinguishes convergent sequence from divergent sequence.

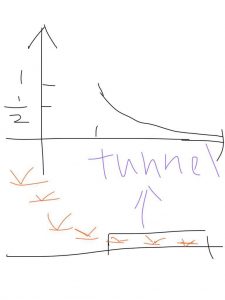
Consider a sequence as a group of birds they fly follow a certain line or curve,and there is a very small space which can be considered as a tunnel .To say a sequence converges, thats to say no matter how small the high of the tunnel is the first bird of its fly curve or line lead the group can toward inside it.To say a sequence diverges,thats to say they fly as high as they want ,and the w first one  of birds refuses to fix their line in a small space(the small tunnel), therefore, they fly randomly or fly higher as they like.

Example:sequence 1/n converges.

1The distinguish convergent series from divergent series.

Assume that a number in a series is not a point but  is a space like a box,every box shows the magnitude of the sum of that part.Imagine we have a room with fixed space.If people can move all those boxes inside that room no matter how many the boxes are without beyond the room,we can say those space sums of those boxes are close to a fixed number and the series converges.Otherwise, those box can not be but in a fixed space room ,the sum of their space are bigger than the room has and it when numbers of boxes increase ,the sum increases,too.Therefore ,in this condition, we can say the series  diverges.