Bai Jingwen(Vivienne): 55932164,Li Mengmeng(Astrid): 59418160,Lu Xuechun : 41519166,Xu Cuishan (Tracey ):32182164
Integration and anti differentiation are commonly conflated since it’s generally misunderstood that they are both the inverse of differentiation. However, they are totally different in their exact definitions, despite that they are indeed connected in some way. Integration is the process of calculating integrals, i.e. the area under a fixed curve, which is a number. Whereas antidifferentiation is the process of finding the antiderivatives of a function, which are a number of functions. Comparing these two vague definitions, it can be assumed that antidifferentiation is not equal to integration.
What is anti-differentiation ?
Antidifferentiation can be understood as the inverse of differentiation.
For a function f(x), the antiderivative (primitive function) of this function, ![]() , are a group of functions F(x)+C that satisfies the derivative of this group functions is f(x).
, are a group of functions F(x)+C that satisfies the derivative of this group functions is f(x). ![]() . So the antiderivative of f(x) is not unique.
. So the antiderivative of f(x) is not unique.
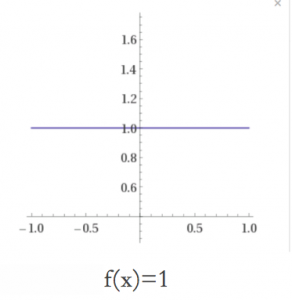
example : 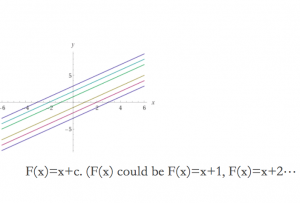
What is integration?
For integration, integral can be defined by Riemann Sum.
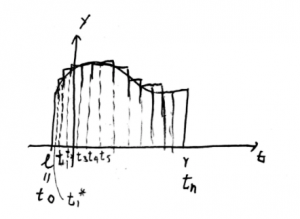
let f(t) de defined on a closed interval [a, b] and divide [a, b] into n subintervals
with the same t value, choose a sample point ti* within [ti-1,ti], so that the area of one rectangles is ![]() ,so the area of these rectangles is
,so the area of these rectangles is ![]() .
.
Given a continuous function f(x) and an interval [a, b], the meaning of integral ![]() is the area of curve trapezoid formed by function f(x), x=a , x=b and x-axis in x-y plane (as illustrated in this picture). So integration is a certain real number.
is the area of curve trapezoid formed by function f(x), x=a , x=b and x-axis in x-y plane (as illustrated in this picture). So integration is a certain real number.
What is the connection between integration and antidifferentiation ?
Integration and antidifferentiation are correlated by Fundamental Theorem of Calculus (FTC) since an integral can be evaluated by using antiderivatives. As FTC2 said, if G(x) is an antiderivative of f(x), then we have,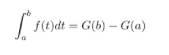
This means to evaluate the integral of continuous function f(x) defined on [a, b], we just need to take antiderivative of the function. In this way, after finding an antiderivative of a function, we can simply plug in x=b and x=a, and subtract these two values. Hence it is where they are connected that antidifferentiation can be used in calculating integrals.
Why students commonly mistake “Integration”& “Antiderivation”?
- Students do not know what is the definition of the two, and get confused whether integration is the same thing as derivation.
- The way to take antiderivative is part of integral (FTC) so students may misunderstand the two concepts.
