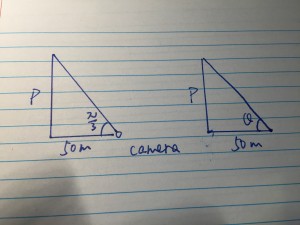
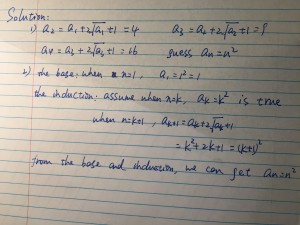The notion of limit dates back to 17th century, which is a sub-product of integral found by Newton, in order to rationalize his second law of force. Even though it seems there is little real life examples of limit itself, limit, however,  is considered to be one of the footstones in the modern mathematics as well as physics.

the notion of limit actually tries to describe a process of approaching. And in mathematics, “How far it is from its destination now” is usually described by an interval. Knowing this, the definition of limit can be presented in an interesting but straightforward way:

For example, in order to show the limit of the function when x approaches “a” is “b”, we can say ,every time I set a boundary of x to show how far it is from “a”(that is x is , say, 2 from “a”), I can definitely set a boundary of y to show haw far it is from “b” (that is, y is, say, 3 from “b”) . If this wordy relationship between x and y is always true (in fact, true forever) during the process of approaching “a” and “b”, we claim the limit of f(x) as x approaches “a” is “b”

If a function is analytic, this means:

1, the function can be differentiated infinite times, and its Taylor series at a point “c” in its domain converges to the function it self for some x in (c-R, c+R). In other words, a analytic function can be written as

,  for all x satisfying

2, the quality mentioned in (1) must be applied to all “c” in the domain of f(x)

Here are some examples:

1, all absolute value functions are not analytic. For instance, f(x)=|x| is not analytic since at  x=0, it is no differentiable, which does not satisfy quality (1)

2, Any function that has some point a where is always true is not analytic except f(x)=0. Since all of these functions’ Taylor series at x=a must be   thus the series fails to converge to the function when  x values are not zero

There are actually no technically difficult questions but ones which require carefulness and patient. What I mean are two specific cases:

The first case, in my opinion, may be the hardest one in the first question. since it has two different characteristics mixing which makes me confused of which technique I should choose. The first impression it left on me was that a normal substitution could not work since the numerator of the function is 1, so I try a trigonometric substitution and totally did twice substitution to finish the problem. However, it turns out that a normal substitution can work and even works more effectively, this surprises me when I redo this question.

The second case is actually very easy but tricky enough to let a student lose some marks since when solving the integration equation and get a function whose derivative is n times itself, most students only come up with a e^x model of f(t), which is generally correct except for the lack of a coefficient. Therefore quite a lot students missed a coefficient of f(t) in their answer.

Study tips:

1, Improve the skill of integrating. In fact, most integration problems don’t require a large amount of thought but sophisticated skill since most of them have evident patterns indicating which technique we should choose. However, such a skill might not come out immediately without sufficient practice.

2, Go over again the way we deal with volume and work problem and form a good habit. Volume problem can be solved in two different ways and both of them have their cons and pros, knowing how they actually work and practicing make us decide which to use quickly during an exam; Work problem can be very abstract so a good way to start is to figure out all the physical stuffs first.

1,  substituting the complex part in the function:

f(x)=x/(1+x^2), let u=1+x^2 , du = 2x dx . There is another strategy that we can tell whether a function is suitable for substitution by thinking what the derivative of the substituted part will look like.  In the case x/(1+x^2), we should notice that the derivative of x^n will lead to nx^(n-1) which implies that the numerator should also contain some similar structure in order to simplify the function. With the same idea, when we substitute sin(x) (cos (x)) we should expect the other part of the function to have cos(x) (sin (x))

2. substitution of trigonometric function:

for functions like f(x)=(sin(x))^m (cos(x))^n or (tan(x))^m (sec(x))^n , we can always do a substitution using the characteristics of their derivative (sin(x))’=cos(x)  (cos(x))’= – sin(x) (tan(x))’ = 1/sec^2(x)  (sec(x))’=sec(x)tan(x).

To be more specific, we divide these functions into two situations:

a) If m and n are all even, then we  can always use 1 + tan^2(x)=sec^2 (x) , sin^2 (x) + cos^2 (x)= 1, cos^2 (x) – sin^2 (x)= cos(2x) to make functions be simplified into the one with single name of trigonometric function and substituted.

b) If one of m or n is odd, then for the trig function with odd power, we “drag out” one of it to make up a form like tan^3 (x)=tan^2 (x) * tan(x), and then the part which is to the power of even number can again be substitute by using  1 + tan^2(x)=sec^2 (x) , sin^2 (x) + cos^2 (x)= 1 and so the function is again simplified into the one with single name of trigonometric function.

3. substitution using trig function

For the function with a part (x^2 + a^2)  (x^2 – a^2) (a^2 + x^2) (a^2 – x^2), we can try to substitute x with asin(x) acos(x)  atan(x) , and therefore simplify the function using  1 + tan^2(x)=sec^2 (x) , sin^2 (x) + cos^2 (x)= 1

To show that a function with finitely many removable discontinuities is integrable, there is some basic knowledge we need to know: 1. a continuous function is always integrable on a close interval. 2. By doing an integral, we actually use lots of small rectangles to partly represent the actual area of a function, and finally take the limit of the width of these rectangles to get an accurate area. 3. A point has an area of zero.

Now when we draws many enough rectangles to represent the area of the function, since there are only finitely many x values at which the function is discontinuous, the rectangles they can “occupy” (means they are in that rectangles) are always finite, and will not increase even we change the rectangles we draw (Again, this is based on the fact we draw sufficiently many rectangles). Now when we begins to reduce the width of the rectangle, notice the number of rectangles occupied is always the same ,and thus the area of them is decreasing. When the width of a rectangle becomes zero by using limit, the whole curve is included and thus integrable except the places where the function is not continuous. However, at this position, the width of the rectangle has already been 0 ,and therefore, becomes a point. And a point has an area of zero ,which is not effected the original area of the function.

You are now a traffic policeman in UBC, and you wanna determine whether someone breaks the traffic rule. You set a camera 50m away from the road, which can automatically track cars passing by. There was once upon a time when you saw a cool Lamborghini passing by. Thinking that it was abnormal, you quickly checked the camera and it recorded that it rotated at a constant speed of 1/10 rad per second and went through 60 degree clockwise from the line vertical to the road. You knew the restricted speed at the campus is 30km/h, and wanted to determine whether the car broke the rule.

let the distance the car has traveled be P and the angle the camera has rotated be Θ,by drawing a triangle ,we can get  a  relation P/50=tanΘ. We differentiate both sides and get

1/50 dP/dt=sec²Θ dΘ/dt, we know dΘ/dt is 1/10 rad/s and since f(Θ)=sec²Θ is increasing in the interval [0,π/3]. So the biggest speed detected, which is dP/dt, appears at the time when Θ is π/3. sec²(π/3)=4  , so dP/dt (at Θ=π/3) =4×50×1/10=20m/s= 72km/h>30km/h. So the car broke the traffic rule.

a) The claim can be transferred into this way : think about that point “0” on the circle has a temperature T(0) and point “兀” has a temperature T(兀). So it is obvious that we only have three situations: 1) T(0)=T(兀) 2) T(0)<T(兀) 3) T(0)>T(兀) . And now let’s discuss them.

1) if T(0)=T(兀), that means point “0” and its antipodal point “兀” has the same temperature,the claim is true

2）if T(0)<T(兀), let’s think about a smooth curve f(x)=T(x)-T(x+兀) so it is obvious that f(0)<0 and f(兀)>0(f(2兀)=f(0) for it is a circle), for f(x) is a continuous function, that is, f(x) can be every value between f(0) and f(兀). And since f(0)<0 and f(兀)>0 , 0 is included in the interval (f(0),f(兀)). We can find that there must be some value a such that f(a)=0. Otherwise , that means f(x) is disconnected in 0, and thus f(x) is discontinuous which is contradictory.

3) the same as the second situation.

so to draw a conclusion there must be a such that T(a)=T(a+兀) on a circle

b) My explanation rely heavily on continuity

1)For example, we wanna set up a rectangle field (instruct the length is x and the width is y ) with a stationary area S,then we can consider  the length(x) is an independent variable and the width(y) is the function of the length, giving the function:y=S/x(x>0).

In this case ,we can see the y approaches to 0 when x gets sufficiently large. So the horizontal asymptote of y=S/x is y=0

2)Think about a chocolate that is bisected many times,instruct the initial block of chocolate is 1,then the size of it becomes 1/2 after being bisected once ,and 1/4 after twice…

so, we can make a sequence for the remain size of the chocolate after being bisected n times:

(1/2)^n. We can notice that chocolate has the trend of decreasing when the times of bisecting increase. So the chocolate approaches 0 when n gets sufficiently large. (1/2)^n converges to 0

3)Think about n year after saving a sum of money in a bank(named as “a”) and the interest rate is “p”, then the first year we get interest ap , the second year we get total interest ap+ap(1+p),the third year…

so the nth year we get the total interest: ap+ap(1+p)+ap(1+p)^2+ap(1+p)^3…+ap(1+p)^n. it is worth of pointing out that it is a geometric series(the partial sum of sequence ap(1+p)^(n-1) ),because the common ratio of the sequence is (1+p)>1 so that series diverges

Hi,everyone , this is my blog in UBC. Math 100 is a cool course