Author Archives: Sabrina Holat

Final Analysis

Leave a reply

 

The path I examined with this e-folio investigates using technology effectively to teach Math and Science.  This includes attention to specific technologies, methods of instruction and even tasks with the technology themselves.  These specific questions come to mind for any teacher who wants to be effective within their teaching methods.  The goal is to provide instructional opportunities where students are engaged in activities while utilizing technologies that provide social and cognitive affordances that foster deep and meaningful knowledge construction which can be recalled.  For this inquiry, it is essential to start with my own view of the role that technology plays in the Math and Science classroom.

My view before this course was generated from my lack of experience, the angst of the unknown, and job time constraints that wouldn’t allow research to ensure proper integration of the technology.  I was accounting for all possible factors and obstacles (such as resources, accessibility…) to protect my lack of technology use and my uneasiness of using technology.  It is pointless to use internet resources for the sake of using technology which ends up losing the students or wasting time.  I was apprehensive with using technology out of context or not connecting with the best possible use for the class.  It seemed easier to let the teacher use the technology to show the class exactly what needed to be emphasized.

The remainder of this analysis will work through a few themes that presented themselves in moulding my view over the duration of this course.  My analysis will explore the influences of PCK and TPACK, knowledge construction, visualization, and real-world connections, and finish with a conclusion.

Once the concepts of PCK and TPACK were introduced, these ideas became a backbone for the remainder of the course and how I analyzed any new information and applications.  It wasn’t until this course that I really grasped what PCK is and how it equips a teacher with the best teaching strategies. The Math and Science concentration of 533 let me dig into actual examples and contexts to realize the power of PCK.  Shulman (1968) argued for PCK to be considered the content knowledge that deals with the teaching process, versus two mutually exclusive domains. Mishra & Koehler (2006) present the need for teachers to have knowledge of the most effective teaching strategies that can help counter student misconceptions and how this needs to be a part of the definition of PCK.  Transforming a subject so it can be taught to others includes much more than just presenting it to the learner.  It involves organizing, adapting and incorporating the most powerful teaching strategies to recall prior knowledge, handle misconceptions, and create connections to new knowledge.

TPACK “is an understanding that emerges from interactions among content, pedagogy, and technology knowledge” (Koehler, Mishra & Cain, 2013, p. 16). This brief description steers educators to understand the intricate relationships formed in the intersections of the components and their applications.  An educator’s TPACK is continuously under renovation as the rapid changes in technology force rearrangement of the other components. In my consideration of TPACK, I am drawn to the idea that effective teachers utilise TPACK every time they teach, and every scenario coupled with every unique teacher means that there are endless applications of what TPACK looks like in the classroom.  While technology has numerous cognitive affordances, I keep in mind an underlying principle of the course; the educator must always be cognisant of TPACK to amplify learning.  “The teacher, through the use of appropriate software, must create an environment that provides context-embedded situations, so that students may work successfully within their zones of proximal development to construct meaningful” knowledge (Dixon, 1997, p. 357).

A topic that encouraged change in my view of technology in the Math and Science classroom is knowledge construction.  The design of a TELE is imperative to how a learner will construct new knowledge. The readings and experiences in the course shaped my ideal TELE design which should be planned so it supports: 1) inquiry and exploration to acquire new knowledge 2) collaboration to construct and integrate the knowledge and 3) creation to showcase the learners understanding or application of the knowledge.  Technologies used in TELEs can be thought of as vehicles whose “functionality relies not only on their attributes but also on their context, the logistical systems and infrastructures that afford their functionality” (Jonassen, Campbell & Davidson, 1994, p. 38).

Once an ideal TELE is in place, an educator must consider the framework(s) that they intend to use.  The GEM framework is a framework that I could use within my pedagogy.  GEM promotes fundamental processes of inquiry including students finding patterns in information, generating hypothetical relationships involving multiple variables, coordinating theoretical models with information and making predictions (Khan, 2007).  The cyclical process that GEM undergoes allows the learner to carry out iterations of the evaluation and modification of their hypothesis.  A teacher’s role during this iterative process can help guide the learner to further analyse and question the hypothesis every time.  T-GEM TELE’s use model-based inquiry as one foundation and the combination of “modeling and inquiry facilitate the development and revision of abstract concepts and, as such, can be considered as a joint educational endeavor” (Khan, 2007, p. 899).

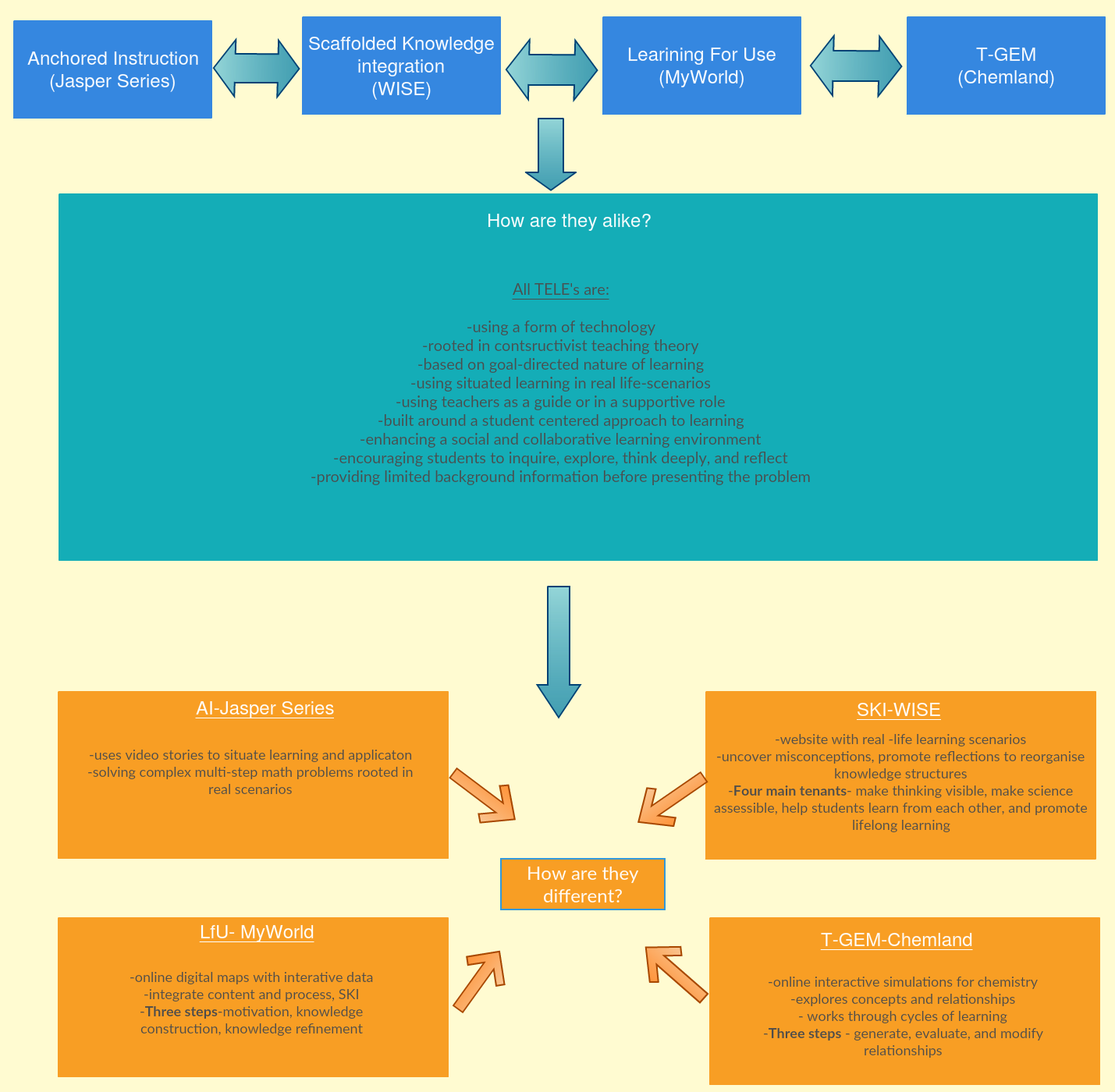
Module B helped me compile a database of foundational design principles for a TELE in the Math and Science classroom. The TELEs that I will use in my future practice will be rooted in constructivist theory, based on a goal-directed nature of learning, use situated learning in real life scenarios, cast the teacher as a guide in a supportive role, have a student-centered approach to learning, enhance a social and collaborative learning environment, provide limited background information before presenting the problem, and encourage students to inquire, explore, and reflect.  I was drawn to SKI and T-GEM design principles because I could anticipate the use of them in my own Math and Science classes. I appreciate the LfU and T-GEM design principles because they are based on a learning approach where knowledge construction is not neat or disconnected. “The construction of understanding is a continuous, iterative, often cyclical process that consists of gradual advances, sudden breakthroughs, and backward slides” (Edelson, 2001, p. 377).  Being educated in a system that was orderly and structured I found Edelson’s words assured me that present and future learning in my classroom can be messy but effective.

Deliberating on AI, I regard this as one of the most effective ways to support my learners with their problem-solving struggles.  As students reach middle school, interest and motivation in mathematics drastically decline and working with unmotivated students becomes the largest challenge during these years (Chao, Chen, Star & Dede, 2016).  As one study reports AI instruction created a motivating environment to learn in for all abilities of students, problem-solving and thinking skills increased and the group interaction supported generative learning as they worked together to create problem structure (Shyu, 2000).

Module C refined some details concerning important characteristics of learning in the Math and Science classroom.  My exploration of embodied learning and information visualization expanded the importance of visualization when teaching and learning Math and Science concepts.  Information visualization technologies help students visualize what is unseen by the eye. These representations show the interactions within relationships in the real world.  I experienced this first hand while playing with Energy Skate Park PhET simulation.  The simulation had many ways to show how energy is transferring as the person skates along the ramp.  A common misconception that students have about energy, is that it gets used up instead of transferring because they cannot see it.  Interactive simulations allow students to access the concept of all energy being transformed, not created or destroyed, allowing “students to study concepts that are otherwise hidden” (Finkelstein et al., 2005, p. 7).  The visual display helps students address their misconceptions.

My view of teaching and learning with technology in the Math and Science class now initiates from the fact that it is beneficial to all learners.  Even with time constraints, careful integration tailored to learning outcomes still proves to help students construct knowledge.  I have observed the use of online resources and applications which are generally well planned and set up for maximum student engagement.  I can express that navigating through using technology and online collaborative environments imparts students with skills that are transferrable to real-life and their futures.

For my personal learning about using technology in the Math and Science classroom, I have been able to connect with a few key ideas that I have broken into manageable pieces for my practice.  I envision myself having the knowledge and confidence to integrate technology into my teaching pedagogy (for math or science) as in the following few examples.  I think the design principles of T-GEM, SKI, and AI fall in line with how I view teaching and learning and would use them to integrate TELEs.  I would specifically use PhET simulations in my lessons either to show during notes or lecture, as a lab, as homework, or as a collaborative class activity.  I view the WISE resource to be helpful in alternate learning scenarios with students who may have extenuating circumstances.

In the past, I have used manipulatives to help students visualize abstract concepts but with an intentional structured pedagogical approach to enhance abstract learning.  It is common for students and teachers to use gestures while explaining themselves, but I see a TPACK opportunity to use manipulatives and possibly digital objects to encourage abstraction of concepts (such as rotation or symmetry) in junior math.  This complies with the constructivist influence on my pedagogical philosophy, particularly “since learning arises form adaptation to the environment” (Winn, 2003, p. 23).

My teaching practice has been impacted in a way that I feel secure in my knowledge about the affordances of technologies integrated appropriately within the classroom to give students the opportunity to construct meaningful knowledge.  This overall goal for the best learning experiences that result in effective student knowledge construction is the driving force behind my inquiry in this e-folio.  I look forward to the analysis I will conduct with every opportunity to integrate technology into my pedagogy since this will further strengthen my TPACK.

 

References

Chao, T., Chen, J., Star, J., & Dede, C. (2016). Using Digital Resources for Motivation and Engagement in Learning Mathematics: Reflections from Teachers and Students. Digital Experiences In Mathematics Education, 2(3), 253-277. doi: 10.1007/s40751-016-0024-6

Dixon, J. (1997). Computer Use and Visualization in Students’ Construction of Reflection and Rotation Concepts. School Science And Mathematics, 97(7), 352-358. doi: 10.1111/j.1949-8594.1997.tb17376.x

Edelson, D. (2001). Learning‐for‐use: A framework for the design of technology‐supported inquiry activities. Journal Of Research In Science Teaching, 38(3), 355-385. doi: 10.1002/1098-2736(200103)38:3<355::aid-tea1010>3.3.co;2-d

Finkelstein, N., Adams, W., Keller, C., Kohl, P., Perkins, K., & Podolefsky, N. et al. (2005). When learning about the real world is better done virtually: A study of substituting computer simulations for laboratory equipment. Physical Review Special Topics – Physics Education Research, 1(1). doi: 10.1103/physrevstper.1.010103

Jonassen, D., Campbell, J., & Davidson, M. (1994). Learning with media: Restructuring the debate. Educational Technology Research And Development, 42(2), 31-39. doi: 10.1007/bf02299089

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905. doi: 10.1002/sce.20226

Koehler, M., Mishra, P., & Cain, W. (2013). What is Technological Pedagogical Content Knowledge (TPACK)?. Journal Of Education, 193(3), 13-19. doi: 10.1177/002205741319300303

Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017-1054.

Shulman, L.S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4 -14.

Shyu, H. (2000). Using video‐based anchored instruction to enhance learning: Taiwan’s experience. British Journal Of Educational Technology, 31(1), 57-69. doi: 10.1111/1467-8535.00135

University of Colorado Boulder. (ND). PhET Interactive Simulations: Energy Skate Park. Retrieved on March 27, 2019 from  https://phet.colorado.edu/en/simulation/legacy/energy-skate-park

Winn, W. (2003). Learning in artificial environments: Embodiment, embeddedness, and dynamic adaptation. Technology, Instruction, Cognition and Learning, 1(1), 87-114.

 

InfoVis Reflection

Leave a reply

Why is visualization necessary for student understanding of math or science?

Throughout our readings and discussions on information visualization, I found time to reflect on why visualization may be necessary for understanding concepts in Physics.

I chose to examine the PhET simulations (specifically for Physics) to research my inquiry. I took the time to read some preliminary pages on the PhET research page on their simulation design process and the thoughts behind their interface.  These simulations are created, designed, tested, and studied with student-centered learning, engagement, and exploration as their foundation (“PhET Look and Feel and PhET Simulation Design Process publications”, n.d.).

Visualization is necessary for understanding concepts in Physics.  Simulations can connect the learner to what the eye cannot see.  Ideas like the conservation of energy or electron flow in a circuit are difficult to imagine with a learner’s own comprehension.  Perkins et al., (2006) make a strong point by explaining how teachers have difficulty creating a shared visual model for their students.  Using sims eliminates this difficulty and allows “the teacher and students to focus their time and attention on creating an understanding of the physics rather than on establishing a common picture” (Perkins et al., 2006, p. 19).

Sims allow learners the opportunity to primarily investigate conceptual knowledge with idyllic conditions and then integrate complex conditions that are typical of real-life (Perkins et al., 2006).  In the sim Energy Skate Park, the skateboarding ramp is a simple parabolic shape with a frictionless surface.  Later, students can add on to the skate ramp, introduce friction, change the mass of and the object skating, view different graphs of the energy levels, and use different gravitational forces from the moon or Jupiter.

When pedagogically integrated into the right context and structured by specific learning outcomes, sims can surge student access to physics notions by interacting with the models which facilitate connections between the students’ everyday understanding and physical principles (Finkelstein et al., 2005).  Sims can provide a visual context for some misconceptions that students may hold to.  Another simulation that I examined (Circuit Construction Kit), which lets students create electrical circuits with required parts, has the option of showing electron flow.  This small change of electrons flowing instead of arrows which represent current flow can help students realize that electrons do not get consumed in a light bulb (Finkelstein et al., 2005).  Often details like wire insulator color can distract or mislead students, especially since resistors have color coding on them.  The simulations “scaffold students’ understanding, by focusing attention to relevant details” (Finkelstein et al., 2005, p. 7).

From my experience with these two specific sims, I have been able to find areas where their integration within a lesson would be conducive to student engagement and construction of knowledge.  These sims need not only be used as a virtual lab, but perhaps embedded within a lecture, used as resources in tutorials, and possibly even as homework.

As an educator, an important pedagogical step to consider is assessment.  While the Energy Skate Park and Circuit Construction Kit sims did not have any embedded self-check points, the teacher needs to incorporate these into the use of the sims.  Whether a simulation has self-assessment constructed within it or the teacher employs their own method of concept check, it is imperative that the learner builds the correct knowledge and leaves the simulation with that.

References

Finkelstein, N., Adams, W., Keller, C., Kohl, P., Perkins, K., & Podolefsky, N. et al. (2005). When learning about the real world is better done virtually: A study of substituting computer simulations for laboratory equipment. Physical Review Special Topics – Physics Education Research, 1(1). doi: 10.1103/physrevstper.1.010103

Perkins, K., Adams, W., Dubson, M., Finkelstein, N., Reid, S., Wieman, C., & LeMaster, R. (2006). PhET: Interactive Simulations for Teaching and Learning Physics. The Physics Teacher, 44(1), 18-23. doi: 10.1119/1.2150754

PhET Look and Feel and PhET Simulation Design Process publications. Retrieved from https://phet.colorado.edu/en/research

University of Colorado Boulder. (ND). PhET Interactive Simulations: Energy Skate Park. Retrieved on March 27, 2019 from  https://phet.colorado.edu/en/simulation/legacy/energy-skate-park

University of Colorado Boulder. (ND). PhET Interactive Simulations: Energy Skate Park. Retrieved on March 27, 2019 from  https://phet.colorado.edu/en/simulation/legacy/energy-skate-park

 

Embodied Learning

Leave a reply

Embodied learning does not seem like the typical pedagogical teaching strategy that would be used in secondary STEM classrooms.  The readings and discussions this week have brought my attention to how embodiment occurs in a math classroom by way of gestures, and how their encouragement can be effective for knowledge construction.  More specifically, I focussed on the use of gestures and their role in conceptualization and abstraction in mathematical contexts.

Seeded in roots of constructivism, Winn (2003) reminds us “that learning occurs when people adapt to their environment” (p. 3).  When people adapt to their environments they are embedded and physically active within their educational setting.   A learner’s mental representation takes on the form of associative networks with a neurological basis that is activated by sensory inputs. (Winn 2003).

Sabena (2004) comments that gestures can help with conceptualization in a functional context. She points out that the internal and external dimensions of gestures are entwined and affiliated.  This affiliation boosts “individuals’ thinking processes and develops a shared semiotic system in which other signs can emerge” (Sabena, 2004, p. 7).  In the case of high school students trying to construct the meaning of an integral from the concept of area while studying graphs from paper, they utilized iconic-representational gestures to describe the new functional relations.

Novack et al., (2014) establish that concrete movements (actions and gestures) connect the learned knowledge to the specific learning context and movement towards abstract gestures situates the learning in a generalized context. The use of different types of gestures amplifies varied levels of conceptual abstraction. A blended approach or “concreteness fading” is a premier practice to facilitate learning, especially for students who are struggling with the concept (p. 6).  To further help a student create understanding, an educator can speak a word while using an abstract gesture.  Novack et al., (2014) hypothesize that doing so can “help a learner integrate and internalize those words” (p. 7).

An example of a way to integrate learning embodiment into my practice would promote the use of actions/gestures in the pedagogy when covering rotation/symmetry in junior math. I could let students use manipulatives to physically maneuver (concrete action) to explore rotation or symmetry. The concrete actions are effective for understanding specific contexts, but lack in promoting student understanding to a general or abstract level.  So, I could introduce concrete gestures (which mimic hand movements of action), guiding students to maneuver their hands as if they were manipulating the object (Novack et al., 2014). Finally, I would have students explore abstract gestures (perhaps just circling a finger) to represent the initial actions and use words such ‘about the x-axis’ while doing so. This example specifically uses the concreteness fading technique mentioned above.

References

Novack, M. A., Congdon, E. L., Hemani-Lopez, N., & Goldin-Meadow, S. (2014). From action to abstraction: Using the hands to learn math. Psychological Science, 25(4), 903-910.

Sabena, C. (2004). The role of gestures in conceptualization: An exploratory study on the integral function. In M. Hoines & A. Fuglestad (Eds.) Proceedings of the 18th Conference of the International Group for the Psychology of Mathematics Education, 4, 145-152. Bergen, Norway: Bergen University College.

Winn, W. (2003). Learning in artificial environments: Embodiment, embeddedness, and dynamic adaptation. Technology, Instruction, Cognition and Learning, 1(1), 87-114.

 

Synthesis Forum

1 Reply

 

Synthesis

This module has challenged my thought process behind how I teach math/science concepts in my classes. While most teachers want to incorporate inquiry-based projects and learning, I feel that Math teachers especially struggle with this.  Understanding the design principles behind these four TELE’s increases a teachers TPACK and confidence to use technology in the classroom. I found myself reflecting on which TELE design would best be suited for which topic in math/science. For example, using a T-GEM TELE to teach concepts in Math (such as exponent rules) where students are encouraged to create the relationships, then test and modify, allow the teacher to exercise strength in TPK and students the opportunity to learn effectively. T-GEM TELE’s use model-based inquiry as one foundation and the combination of “modeling and inquiry facilitate the development and revision of abstract concepts and, as such, can be considered as a joint educational endeavor” (Khan, 2007, p. 899).

After this module, I feel it is easier than I thought to incorporate TELE’s into teaching concepts, especially in science.  The lesson needs to provide minimal information to equip the students to inquire in a social and collaborative environment. The WISE project I explored was an engaging application that helped students uncover their misconceptions and reorganize their learnings with scaffolded knowledge integration where needed.  T-GEMs are an effective addition to help students really understand science concepts because of their design principles with discovering relationships.

Anchored instruction would be effective to facilitate students to solve complex multi-step problems in a social and collaborative setting. This type of TELE could be used in any Math classroom and would especially be effective in a senior level math class, where students are applying concepts from years of math learning and not necessarily specific unit concepts.

Reference

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905. doi: 10.1002/sce.20226

T-GEM Integration

Leave a reply

Students usually encounter difficulty when learning exponent laws in junior math classes.  Whether it is related to keeping the laws straight in their heads, applying them, or conceptually understanding what is really happening.  I identify this as a challenge from the numerous quizzes and tests that I have marked over the years.  Like other challenges in math class, I often see students memorizing the rules so that they can apply them to get marks.  For some teachers, the difficulty in this topic lies in finding a way for students to construct their understanding.  Usually, teachers will show what the rule is and how it works and then let the students practice.

I found a desmos activity that is not necessarily a simulation, but an interactive resource that engages students in creating and understanding the exponent laws.  The students start with compiling cards with various representations of exponents into like piles, I would insert group collaboration to compare and generate the exponent rules.  Then students have a few more activities (that are submitted to the teacher) which encourage reflection of the exponent laws, or evaluation.  Next, students are asked to create their own expression with an answer key and submit to class for more collaboration. This step can encourage modification of the rules if students are encountering incorrect answers. A final challenge can solidify any changes to the initial rules.

*Not sure if other math teachers have seen this resource https://teacher.desmos.com/

GEM visual.png

SKI, WISE, & LfU Reflection

Leave a reply

WISE is a customizable platform created by professionals from the educational, technological, and scientific fields that is a resource which uses the internet and various interactive activities to facilitate students in knowledge construction.  It is founded on principles of the SKI framework, cognitive apprenticeship, and constructivist pedagogy.  SKI promotes knowledge integration through its technological and curriculum design in four major ways.  SKI make science visible or identifies new goals for learning, makes thinking visible, provides social supports and helps students learn from each other, and it promotes lifelong autonomous learning.

While both WISE and the Jasper series are intended to engage a student in inquiry-based learning, they clearly have their differences.  WISE is a more modern approach that integrates interactive technology to facilitate knowledge construction.  The Jasper series is a narration or story in which a problem unfolds that students need to solve, whereas WISE is a series of activities that take the student on a learning journey in a more structured format.

I think WISE projects would make for excellent resources for students with alternate learning scenarios, whether it be students with learning difficulties or students who miss a lot of school because of sports or health situations.  WISE’s customizability is an amazing feature that puts the teacher in the designing chair so a project can be changed according to its intended use to suit the needs of the learners or teacher.  At this point with my limited exposure to WISE, I don’t think I would change anything, but rather make more projects available covering more subjects and grade levels.

LfU Forum Post

Leave a reply

In what ways would you teach an LfU-based activity to explore a concept in math or science? Draw on LfU and My World scholarship to support your pedagogical directions. Given its social and cognitive affordances, extend the discussion by describing how the activity and roles of the teacher and students are aligned with LfU principles.

I would incorporate Google Earth into an inquiry project where the students are challenged to find two or more different shaped real-life world structures (solids) that have the same volume or surface area.  It would be ideal to infuse many opportunities for collaboration/discussion amongst the students when possible. These communications do not necessarily need technology, but rather an opportunity to communicate ideas, difficulties, arguments, and connections.

Motivate

The context of the inquiry itself creates demand.  Students will need to calculate surface areas and volume to complete the task. Using Google search can give students a starting point from which they can build hypotheses and initial projections.  The initial research may present a gap in their knowledge with calculating surface area or volume of real-life world structures which elicits curiosity. Through the process of making predictions students will be relying on prior conceptions.  Edelson (2001) declares that “articulation of prior conceptions has been recognized as a valuable technique for identifying potential misconceptions and for activating existing knowledge structures to which new knowledge can be connected” (p. 376).

Knowledge construction

Using Google Earth allows students to compare, take measurements, and observe the solid structures from all over the world via firsthand experience, which could not be done otherwise. Students or teachers may interact with media or each other to foster communication to support knowledge construction.  I think it is important to note that knowledge construction does not always happen on the first exposure of a step by step process.  Often it is a “continuous, iterative, often cyclical process that consists of gradual advances, sudden breakthroughs, and backward slides” (Edelson, 2001, p. 377).

Knowledge refinement

Through reflection and application, students can refine their knowledge so it is established for future retrieval and use (Edelson, 2001).  I would use structured journal entries for students to compile a project journal that they can use to share and discuss with other students. Other teachers or disciplines may choose to use a collaborative learning environment that would facilitate discussions.  I would specifically have students compare their initial projections with their results and reflect on how the thought process has changed in making those predictions.  The students would also use applications that would enable them to create a final presentation of their reflections including their initial/final thoughts. This last step allows technology to be a tool of necessity for students to apply their newly constructed knowledge.

While this activity does not factor in GIS software, this concept is related to spatial literacy.  A teacher may wish to expand on connections to spatial literacy, especially since Google Earth may be a suitable tool to do this with. Realistically, “a spatially literate workforce and citizenry able to access, manage, visualize, and interpret information, also capable of multidimensional thinking, are vital to… address the world’s complex problems (Perkins, Hazelton, Erickson & Allan, 2010, p. 213).

References

Edelson, D. (2001). Learning-for-use: A framework for the design of technology-supported inquiry activities. Journal Of Research In Science Teaching, 38(3), 355-385. doi: 10.1002/1098-2736(200103)38:3<355::aid-tea1010>3.0.co;2-m

Perkins, N., Hazelton, E., Erickson, J., & Allan, W. (2010). Place-Based Education and Geographic Information Systems: Enhancing the Spatial Awareness of Middle School Students in Maine. Journal Of Geography, 109(5), 213-218. doi: 10.1080/00221341.2010.501457

PCK & TPACK

1 Reply

PCK is essentially how subject material is presented to students for learning. Specifically, how “the teacher interprets the subject matter and finds different ways to represent it and make it accessible to learners” (Mishra & Koehler, 2006. p. 1021). Shulman (1986) presents the urgency for teachers to have knowledge of the most effective teaching strategies that can help counter student misconceptions and how this needs to be a part of the definition of PCK. This thought resonated with me, especially since the beginning of Module A of this course started with misconceptions in math and science classrooms.

TPACK “is an understanding that emerges from interactions among content, pedagogy, and technology knowledge” (Koehler, Mishra & Cain, 2013). This brief description steers educators in the direction of having knowledge of the three individual components, but more so understanding the intricate relationships formed in the intersections of the components, and their applications.  In my reflection of TPACK I was drawn to the idea that effective teachers utilise TPACK every time they teach, and every scenario or context coupled with every unique teacher means that there are endless applications of what TPACK looks like in the classroom.

An example of PCK that came to mind for this post is using BEDMAS to help teach the order of operations in algebra.  That to me is an example of a generic pedagogy used to teach math content.

References

Koehler, M., Mishra, P., & Cain, W. (2013). What is Technological Pedagogical Content Knowledge (TPACK)?. Journal Of Education, 193(3), 13-19. doi: 10.1177/002205741319300303

Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017-1054.

Shulman, L.S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4 -14.

Anchored Instruction Symposium

1 Reply

There are a few commonly acknowledged issues surrounding motivation, level of understanding and knowledge application when teaching and learning mathematics. As students reach middle school, interest and motivation in mathematics drastically declines and working with unmotivated students becomes the largest challenge during these years (Chao, Chen, Star & Dede, 2016). Students are gaining knowledge at surface levels to jump through assessment hoops, leaving them unsure of why they are learning math concepts or how to apply the concepts in their lives.  It is inarguably important to develop component skills, especially in the context of meaningful problem posing and solving activities (Cognition and Technology Group at Vanderbilt,1992a). The culmination of these issues results in students who are unmotivated, uninterested, and lack thinking and problem-solving skills.  I have first hand experience with students who have factual mathematical knowledge but are not able to use it towards solving word problems either because they don’t know how to, or they become super anxious.  Typically, learners do not know how to apply their learned knowledge to find solutions.

In these situations, the role of the teacher is best enhanced with strong pedagogical content knowledge (PCK) because the teacher “interprets the subject matter, finds multiple ways to represent it, and adapts and tailors the instructional materials to alternative conceptions and students’ prior knowledge” (Koehler, Mishra & Cain, 2013, pp. 15).  PCK can help the educator find effective teaching strategies such as anchored instruction for learning math concepts.  Grounded on theories of constructivism, situated learning, and cooperative learning, anchored instruction (AI) provides opportunities for learners to use generative learning in real-life inquiry scenarios. Park and Park (2011), solidify that using problem-based learning in schools creates an avenue for student to experience real-life problems.  The latest literature that I have read reports increased positive feeling towards using AI to learn. Specifically, AI instruction created a motivating environment to learn in for all abilities of students, problem solving and thinking skills increased and the group interaction supported generative learning as they worked together to create problem structure (Shyu, 2000).

The Jasper materials are designed in such a way that they can meet requirements of the above-mentioned grounding theories of AI.  They have real world contexts that support complex, open-ended problem solving, communication, and reasoning; more connections from mathematics to other subjects and to the world outside the classroom (Cognition and Technology Group at Vanderbilt,1992a).  The key issues of motivation and interest are targeted by the seven design features specific to AI.

For the purpose of mathematical instruction, contemporary videos do not address issues raised in this post when stacked against the Jasper series videos. Contemporary videos might use current technology that offer other affordances, however, they all are based on direct teacher led instruction of mathematical concepts.  They are created for brushing up skills, supplementing teacher instruction, cramming for tests, or supporting weaker students.

References

Chao, T., Chen, J., Star, J., & Dede, C. (2016). Using Digital Resources for Motivation and Engagement in Learning Mathematics: Reflections from Teachers and Students. Digital Experiences In Mathematics Education, 2(3), 253-277. doi: 10.1007/s40751-016-0024-6

Koehler, M., Mishra, P., & Cain, W. (2013). What is Technological Pedagogical Content Knowledge (TPACK)?. Journal Of Education, 193(3), 13-19. doi: 10.1177/002205741319300303

Park, K., & Park, S. (2011). Development of professional engineers’ authentic contexts in blended learning environments. British Journal Of Educational Technology, 43(1), E14-E18. doi: 10.1111/j.1467-8535.2011.01244.x

Cognition and Technology Group at Vanderbilt (1992a). The Jasper experiment: An exploration of issues in learning and instructional design. Educational Technology, Research and Development, 40(1), 65-80. doi: 10.1007/bf02296707

The Design of TELEs

Leave a reply

From all the tidbits that I include in my mind that help define technology, I would say it is something that can support meaning making by students when students learn with rather than from technology by utilizing tools and their applications (Jonassen, 2000).  Designers of learning experiences need to know their learners’ strengths/weaknesses, prior knowledge, and a clear precise goal of what they are trying to achieve with their TELE.

The TELE should be designed in a way that it supports:1) inquiry and exploration to acquire new knowledge 2) collaboration to construct and integrate the knowledge and 3) creation to showcase the learners understanding or application of the knowledge.  Technologies in TELEs can be thought of as vehicles whose “functionality relies not only on their attributes but also on their context, the logistical systems and infrastructures that afford their functionality” (Jonassen, Campbell & Davidson, 1994).

References

Jonassen, D. H. (2014). Mindtools (Productivity and Learning). Encyclopedia of Science Education, 1-7. doi:10.1007/978-94-007-6165-0_57-1

Jonassen, D., Campbell, J., & Davidson, M. (1994). Learning with media: Restructuring the debate. Educational Technology Research And Development, 42(2), 31-39. doi: 10.1007/bf02299089