Explanation:

According to the definition of antiderivative and integration, antiderivative is the opposite process of derivative and it was introduced when we discussed the Fundamental theorem of calculus, if the F(x) is the antiderivative of f(x), then the integration of f(x) from a to b equals to the value of F(b) subtract the value of F(a). So basically, the anti-derivative of a function(a) is finding where the function(a) derivative from. In the sense that if function(b) experience derivative can get function(a), so that function(b) is the antiderivative of function(a). Besides the antiderivative is also been called indefinite integrals.

 

And for the integration, it is a basic and fundamental part of calculus and this includes different types of integrals. We started to learn this from Riemann integration, which is known as definite integral. And this definite integral will end up with a number.

 

In terms of whether a function have antiderivative or not integral or not, if the function is not continuous they don’t have antiderivative. But it may still do integration in terms of definite integral.

 

Example:

In physics, the time-speed question is a really great example to explain the definitions of antiderivative and integration.

For example:

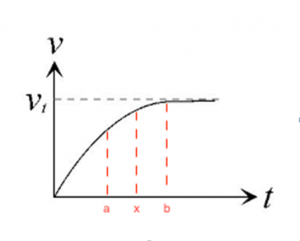
To calculate the distance from time a to b, we need to use the definition of integration. Since a and b are two constants with certain values. From formula d’(t)=v(t),

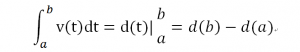
While if we want to express the distance from time a to an uncertain x, the expression of distance is calculated by antiderivative.

Since x is not fixed, the antiderivative of v(t) from time a to x should be d(t). To be more specific, if v(t)=, by the definition of antiderivative , we can get: d(t).

In this way, we can explain the difference between antiderivative and integration.

 

Math 101 Assignment 1

Junqian Hu (22689160) —- Sylvia

Manni Zhang (45580164) —- Manni

Yilun Yang (24307167) —- Alan

 

Part 1: Short Story

Jennie and John are the newlyweds and they plan to construct their house by themselves. Jennie chooses a special type of window with an arched side on top. When they choose the real style, one question comes up: what is the area of their window?

Smart Jennie noticed the small gratings on the window. She says: “Why don’t we divide the windows into small parts and add them up?” She divides the window into two parts: a regular rectangle below and an irregular shape above with an arched top side. Then she divides the above shape into 4 gratings and seems the irregular shapes as regular small rectangles. Approximately, the whole area of the window comes out.

Part 2: Further Explanation

We wanna know the area of this irregular shape, we will cut this area into small pieces of “rectangles” and then find a point from the curve side assume the length from the opposite side of rectangle be the height so that we can calculate the area of each rectangle. Add them up, we can get an approximate value of the area that the irregular shape owned. However, the we don’t think the value is precise enough, we decide to get more small pieces. As more and more pieces we get the more and more accurate the value we get.

As you can see from the graph, the total area of the rectangles nearly equals to the area of the shape.