Overview

Population and household data for Japan’s 2015 census were translated and parsed for variables relative to our vulnerability analysis. All spatial data was projected into the geographic coordinate system JCD 2000 Japan Zone 9. Once data tables with the filtered data were joined with the grid square shape data, the census data was able to be analyzed and visualized in ArcGIS. 

Figure 1. Mesh grid of census polygons for the Tokyo metropolitan area used as the basemap for our analyses. Each polygon is one square kilometer.

Point data showing the location of medical  facilities and polyline data of urban rail networks (both obtained from Open Street Map) were given a buffer of 1 km and overlapping borders were dissolved.  Buffered rail lines and medical facilities were individually intersected with the grid squares populated with census data. As some grid squares were only partially covered with the buffered area, area fractions were calculated for the portions of cells outside of 1 km from medical facilities and railway lines.  Area fractions of all partially covered and completely uncovered cells were included in the weighted multi criteria analysis.

Constructing a Social Isolation Index

In order to construct our isolation index, we identified the ten factors we deemed most important from the census data to which we had access. Originally, we hoped to include economic factors to in order to formulate a housing and economic vulnerability index. However, we were unable to obtain adequate household economic data at our scale of study. Due to this obstacle, we chose to focus on social isolation instead.

After identifying our factors of interest, we weighted them using the analytical hierarchy process (AHP) at http://123ahp.com/ . The factors and their corresponding weights are as illustrated in Figure 1. below:

Criteria Factor	Weight
Single occupant household aged over 65	0.2332
Single occupant household	0.1402
Population of women over 75	0.1155
Population over 75	0.1032
Distance over 1 km from metro line	0.0859
Distance over 1 km from healthcare facility	0.0802
Population of women over 65	0.0750
Two-occupant households aged over 65	0.0747
Population over 65	0.0585
Two-occupant households	0.0337

Figure 2. Isolation index factors by AHP weights, consistency ratio: 0.0503

We assigned weights based on what we felt was appropriate; however, this process was inevitably somewhat arbitrary. While our index is based on indicators of social vulnerability, it is not an empirical identifier of vulnerability to social isolation. The factors we chose, and the way we chose to scale, standardise, and weight them represent only one possibility of a myriad of approaches one could take towards developing a social isolation index.

Since our census boundary data was in vector format, we decided to conduct ‘vector-based’ multi-criteria analysis rather than rasterise the data. This decision meant that we had to standardise a large amount of tabular data in order for the weighted sum to have a meaningful result. We standardised the spatial variables (access to healthcare and transit) by giving each polygon a score based on the inverse of the fraction of area of said polygon covered by the healthcare and transit buffers. This was calculated as follows:

Score = 1 / (a_i / a)

Where:

a_i = the area of the intersect of buffer layer and census grid polygon and where

a = the area of the census grid polygon.

In order to standardise the demographic and household composition data, we first normalised each specific value by the total (e. g. fraction of total population over 65). However, these normalised fractions were not scaled in a meaningful way from zero to one. We therefore classified each factor by deciles; we replace the fraction values with the midpoints of the decile in which each value was found. Thus, values in the first decile were replaced with 0.05, second decile 0.15, third decile 0.25 and so on.

After we had standardised all of our factors, we calculated a weighted sum for each census grid polygon. We repeated this process with equal weights in order to conduct a sensitivity analysis. The raw results of the weighted and unweighted sums are illustrated in Figure 2., where red indicates a high isolation risk and blue indicates a low risk.

Figure 3. Weighted social isolation index (left) and unweighted (right). Red is high risk, blue low risk.

Further Analysis: Hotspots and Grouping

Once the isolation index was finalised, we used it to conduct hotspot and grouping analyses. We decided to use these analyses because tests for spatial autocorrelation of key factors using inverse distance weighting suggested a highly significant degree of clustering. Figure 4. illustrates this high degree of spatial autocorrelation.

	Single-occupant households aged over 65 as ratio of total households	Ratio of single occupant households	Ratio of population over 75	Ratio of population over 65
Moran’s Index	0.102	0.190431	0.0290	0.0210
Expected Index	– 0.000037	– 0.000037	– 0.000037	– 0.000037
Variance	0.000001	0.000001	0.000001	0.000001
z-score	100.010	185.835	32.842	24.507
p-value	0.000000	0.000000	0.000000	0.000000

Figure 4. Spatial autocorrelation statistics of key isolation index factors.

We next conducted hot spot analyses of the weighted and unweighted isolation indices using the optimized hotspot analysis (Getis-Ord Gi* statistic) in Arc. The optimized hotspot analysis identifies statistically significant clusters of high and low values (hot spots/cold spots) of an input variable. The outputs of the hotspot analyses are discussed in the Analysis section.

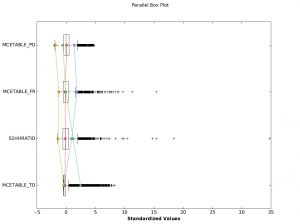
Finally, we conducted a grouping analysis of four isolation factors: total population, single-occupant households aged over 65 as a ratio of total households, single occupant households as a ratio of total households and the ratio of population over 65. These factors were assigned to four groups and no spatial constraint was specified. Figure 5. shows the parallel boxplot of these 4 factors. We conducted a second grouping analysis of all 10 factors in our isolation index, again with no spatial constraint, but allowing Arc to determine the optimal number of groups. The parallel boxplot for this grouping analysis is shown in Figure 6.

Figure 5. Grouping analysis with four variables and four groups. MCETABLE_PO is ratio of population over 65, MCETABLE_FR is the ratio of single-occupant households over 65 to total households, S1HHRATIO is the ratio of single-occupant households to total households and MCETABLE_TO is the total population of each 1km mesh polygon.

Figure 6. Grouping analysis of the 10 factors of the isolation index into two groups: high (blue) and low (red) vulnerability. It is interesting to note that the grouping indicates a spatial correlation of all of our ‘risk’ variables.

Determining Natural Hazard Risk

Using data from the Japanese government’s Ministry of Land, Infrastructure, Transport and Tourism, mass wasting hazard areas were overlaid upon the hotspot analysis.  Because the file provided hazard data in polygons at a very detailed resolution, buffers were added and dissolved to allow adjacent polygons to merge.  Landslide, debris flow, and steep slope hazard areas were buffered 100 m and displayed at 30% transparency in order to observe the underlying data.

A Digital Elevation Model for the country of Japan was reclassified to isolate areas with elevations of 10 m and below.  Cells with low elevations were converted to a polygon layer and symbolized with a crosshatch pattern to allow visual penetration to the underlying social isolation analysis.  Polygon boundaries were smoothed to reduce the sharp boundaries that were produced from converting a raster file to polygon.

Analysis of natural hazards was limited to observation of the spatial relationships between the social isolation hotspot analysis and hazard areas.  In depth analysis of the portion of grid cells within a hazard area were not conducted because mass wasting events typically cover wide reaches and therefore calculating area fractions of cells in a hazard area may not provide a meaningful measure of risk.