
I have to admit I was overwhelmed this week when I was faced with eight (8!) case studies to explore. Thankfully most were quite short, clocking in at less than 30 minutes, and they were actually interesting! I was a little judgemental when the videos seemed a tad dated, but what technology doesn’t seem dated almost immediately these days?
Example 1: I traded in my Pixel last month for a Pixel 2. The original Pixel was only released in October 2016 – barely a year ago.
Example 2: Last term I created tutorial/screencast videos for D2L to help my staff get better acquainted with its basic functionality. When we returned this term D2L Brightspace had upgraded to Daylight, making all my tutorials obsolete, or at least annoyingly dated – nothing looked quite the same.
My point is that I was once quick to judge a video by its video quality and perceived production decade – perhaps our generation’s higher-tech version of “judging a book by its cover” – but these days I’m much more interested to see if the content remains relevant. Often, much of it does, once you get past the initial reluctance.
Among the various cases offered I chose to focus most closely on Case 2, which deals primarily with introducing graphing calculators (namely the TI-83) into class back in 2004 or so. This case struck a nerve because I’ve had conversations and meetings with my department as recently as last Tuesday about the role of the calculator in classes. Opinions range from “they should do it all on paper then check their answers with the calculator!” to “let the calculator do the nitty gritty for them so they can tackle more complex problems!” to “why buy this $240 (in Doha) for a TI-84+ when all students have mobile devices and can get Desmos for free?!”… that last one was me…
Anywho, without further ado:
What are the underlying issues and why are they issues?
From my perspective, the first underlying issue for this case was the fact that it is significantly cheaper to buy a class sets of TI-83 graphing calculators (which the teacher referred to as computers, and he’s not wrong) than to buy a class set of desktop computers. This is a pertinent issue, one even more pertinent circa 2004, when smartphones were not as widely used. Not only do students and their parents rarely have “money to burn” per se, but neither do schools and school boards. If they can choose graphing calculators for mathematics classes for each student instead of expensive desktops, or even laptops, it may help ease the financial strain. One caveat here is that a graphing calculator, like any tech, is not a magic bullet. It must be thoughtfully chosen to meet a specific need of the students. For example, examining course requirements could reveal that a much cheaper calculator like the “Casio Scientific Calculator fx-82AU PLUS II” could do most of the same job at half the cost.
Another underlying issue in this case was that leveraging a tool like the TI-83 can help students from getting “lost in the math”. Instead of trying to “get a number” at the end of a series of steps, the teacher was able to ask deeper questions and the “technology made [the students] comfortable to push this question to the limit”.
How would I explore a response?
Let’s not forget that ”better learning” using a tool like the TI-83 doesn’t happen automatically. Training is required for teachers to understand how to best leverage the tool for the benefit of their students and their unique learning contexts. As was said by Teacher F in the case study, “teachers do need to understand as much of technology as possible to make sure that you are able to ask questions of an appropriate level to get the mathematics out”.
I’d also like return to an earlier point on how TI-83 is a notably cheaper choice for classrooms than individual desktop computers. While this still mostly holds true, there exists stiff competition and excellent alternatives. Chromebooks are now becoming comparable in cost to calculator like the TI-84+, and there exist free mobile apps that can do almost everything that the best graphing calculator could do in 2004. Finally, why focus on a single expensive tool like a TI-83, or invest in static desktops for the classroom, when we could focus on leveraging students’ own existing mobile devices using a Bring Your Own Device model?
What further questions does the case raise?
Many of the questions that came to mind during this case were ones about students. Did the introduction of the graphing calculator increase student engagement? How did students that took math courses using the tool fare against past students who did not have it? Did the school start using the TI-83 for all their math classes? We heard from several students who were doing exceptional work with the calculator (Boba Fett represent!), but how did the weaker students feel about using a tool with so many buttons and functions? Where are all these students now, and what tools do they use for math problems? What would be the 2018 version of Teacher F’s mathematics technology?

How might the issue that is raised exacerbate or ameliorate a conceptual challenge held by students?
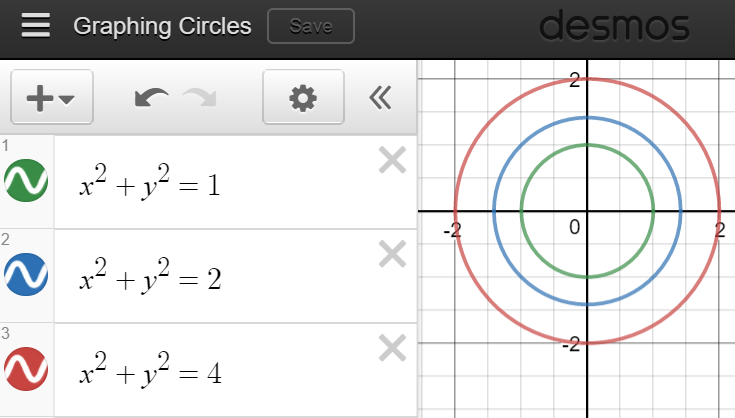
I think that, for most students, once they wrap their head around what a graphing calculator can do it opens the doors to a huge world of conceptual understanding. Ideas that could once only be explained in words, textbook diagrams, or time-consuming hand-drawn graphs could now be visualized with nothing more than a few button taps. For topics like curve sketching, graphing tech allows intimidating, abstract or, confusing equations like
x² + y² = 1
x² + y² = 2
x² + y² = 4
to be seen for what they really are: simple circles.
All in all I feel like using graphing calculators, especially recent free graphing software like Desmos, is nothing but a good thing. I can see it being introduced at extremely early levels of mathematics education, as early as the first few grades, to quash conceptual challenges with graphing equations before they have a chance to even become confusing.
Scott
Hi Scott,
As someone who hasn’t touched a graphing calculator since Math 12, I found your post to be an informative crash course in the current world of graphing calculators! It’s very interesting that free graphing software is available and you’re right, this does make this technology much more accessible. As a grade 6 teacher, your idea to introduce this software at a younger age is interesting. In my class we rarely use basic calculators and I wonder what using it with this age group would look like? I would certainly have to re-familiarise myself with this technology but do think it could bring about exciting curriculum enhancements and, as you mentioned, maybe stop some confusion before it occurs!
Kathryn
Hello Scott,
I always get worried to reply to your postings, they are elegantly worded and usually contains information above my head!! This week is no different! But, here I am replying, not because I have any experience using a Graphing Calculator in the last 20 years, but my daughter said the words “graphing calculator and I need to get one.” Your posting was great timing for me!
I found your reflection of the different Graphing Calculators to be very helpful, it provided an excellent analysis of the different calculators. To be honest, I asked myself, does she really need one? With advanced technology available online, Graphing Calculators seem a bit primitive, however, I could be wrong. I was happy to hear that some free software is available, is it IOS compatible?
I concur that the introduction of any technology (Kahoot, Desmos, etc) can be beneficial to any classroom, as it alleviates the likelihood of misconceptions. I was wondering does Graphing Calculators promote the collaborative learning approach?
Hey Mary – I don’t mean my posts to worry you!! I think when I write my posts sometimes I get lost in it all and have a tendency to write everything that comes to mind while I’m reading, researching, Googling, etc. I can see looking back that it makes for lengthy and perhaps intimidating posts. Maybe that’s something I should work on; concision. In the meantime, I’m really glad you replied!! 😀
To respond to whether your daughter needs one – in general, probably not. There are better and cheaper tools available online and on mobiles, as I mentioned… the (BIG) problem is many teachers give rigid summative math assessments that ban mobiles, allowing only ‘real’ graphing calculators. It’s understandable, it’s hard to monitor every student and make sure they’re truly using their phone/mobile for calculations, but it raises the classic question every reflective teacher often poses: “Isn’t there a better way?”
In short, SHE probably needs one, because her class is likely designed around it, and visualizing and understanding graphs is an incredibly important skill to develop. The earlier the better. However, she should TOTALLY boot up Desmos on her computer or phone during the course and play around with graphs. It’s more user-friendly and more fun. Try matching her class’s topics with the activities here! https://teacher.desmos.com/popular
How it works: https://www.youtube.com/watch?time_continue=1&v=m3RyvbvNAuY
As for iOS compatibility – YUP! Just pop on to desmos.com or download Desmos from the App Store and you’re/she’s off to the races!
She could also use this and use the TI for free: https://www.cemetech.net/projects/jstified
…but you need the ROM… and that’s technically illegal without owning the actual calculator… so… yeah.
Finally, you asked if using Graphing Calculators promote collaborative learning. I’d say yes because, for example, it allows for a much more visual and immediate way for students to compare/contrast solutions. The TI calculator lags here because it is difficult to change simple things without a lot of button presses. I’d may as well continue my Desmos rant here and say that using THAT, along with the teacher’s tools and activities, could allow for a wide variety of collaborative learning opportunities. Here, I made a thing for you: https://www.desmos.com/calculator/irsels8lz6
Follow the link and drag around the button next to “a”. Choose your favourite number. Ask your daughter her favourite number. Set a to both of those and then talk about what’s different, and try to figure out why! You’ve got yourself an activity! haha 🙂
Thanks for your response, I really appreciate it. Have a great weekend!
-Scot
Hey Kathryn, thanks for your response!
I was really surprised to hear that your kiddos in Grade 6 barely use basic calculators! Then I realized I’m probably quite out-of-touch when it comes to Grade 6 students, especially having taught college for the last 5 years! I totally understand the reasoning though – or at least my conception of it – which is to provide students a fundamental basis of knowledge and number sense before allowing calculators to do work for them. Do you allow them to use calculators at all? At this level I think using calculators could be a really neat way of extending problems without bogging down time with the nitty-gritty calculations.
For example, I used to introduce my Grade 6 students to the Fibonacci sequence, then have them add up numbers in Pascal’s Triangle so see if they could find the sequence. Eventually they found the sequence, like this:
https://www.maplesoft.com/view.aspx?SI=3617/pascaltriangle1.gif
I then let them “explore” the triangle by printing out a huge one and having them multiply numbers and such to see if they found more patterns. I also had them try colour coding to see if they saw patterns. I will admit that, in these cases, it was more about exploring numbers and finding patterns than solving questions and delivering a single answer, and so using the calculators was often just a tool to help them find those patterns .. if that makes any sense!!
On another note, I’m not sure if your students learn much about algebra or lines in grade 6 – probably not – but if they do using something like Desmos could be a really neat way to immediately connect algebra to graphs. So many students get all the way through high school without truly understanding how equations and graphs and connected. Might be neat to experiment at this age.. plus, it’s free!! 😀
If you’re interested in learning more check it ouuuut:
Popular Desmos Activities – https://teacher.desmos.com/popular
Desmos Activities Intro – https://www.youtube.com/watch?time_continue=1&v=m3RyvbvNAuY