Author Archives: jan lewis

Augmented Reality Interactive Storytelling (ARIS) for STEM Info-Visualization

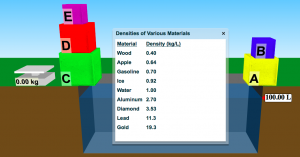
Reflect upon knowledge representation and information visualization by examining a question that you thought about above for the resource sharing forum. In your entry, as you think about knowledge representation and info-vis, ensure that you refer to the software you chose to explore and cite your 2 required readings for this lesson.

Consider the cognitive affordances of the software examined.

Speculate on how information visualization software (name the software) could be embedded in the design of authentic learning experiences and,

Suggest active roles for the teacher and the students, as well as a suitable topic. Endeavour to make connections with your future personal practice in this entry.

The software I added to the Resource Page was the ARIS (Augmented Reality Interactive Storytelling) game engine created by Field Day. This resource affords embodied learning from both the view of embodied as physical movement in the space (Stevens, 2012) and embodied as cognition that is embedded within artificial environments including simulations (Winn, 2003) and situated cognition AR activities (Bujak, et al., 2013). It is extremely versatile for teachers interested in informational visualization in simulations or creating place-based games and explorations. I considered two possible ways ARIS software could be embedded into authentic learning experiences.

Buoyancy & Gravity in Gas

In the Discussion Activity for this lesson, I considered the challenge of understanding the buoyant force for fluids that were liquids. ARIS provides a guided, interactive simulation game that explores the buoyant force in air. In their collection of mini-games set in the comic book world The Yard, students will find Hot Air Balloon which allows learners to explore concepts of air pressure, temperature, buoyancy, gravity and volume as they attempt to fly a hot air balloon longer and longer distances and read the dialogue as the kids from the junkyard try to figure out the science behind it all. As Srinivasan et al. (2006) observe, “Generally speaking, it is less expensive to develop a simulation than to provide real experience” (p.137). Few if any students will have the pleasure of exploring buoyancy and air pressure in a real hot air balloon but such simulations could easily be integrated into a unit for primary children on natural forces or junior students studying flight. Nevertheless, this simulation may not do as well as a stand-alone activity and would be more effective in terms of learning outcomes after students explored real objects and began to be curious. “A learner’s success with learning new material can be described in terms of the learner’s prior knowledge, ability, and motivation (Schraw et al., 2005). Prior knowledge accounts for the largest amount of variance when predicting the likelihood of success with learning new material (Shapiro, 2004)” (Srinivasan et al., 2006). Perhaps including this as part of a WISE project or after building miniature models of hot air balloons and watching a video of real hot air balloons can lead to the question of what it would take to make their models float like the real thing and more importantly, why their models would not float but much larger objects in real life will. As it relates to my own practice as Teacher Librarian, providing those videos or making time to play this game in tandem with their Science teachers’ coverage of these topics (or creating the WISE project) would be a useful incorporation for their Library periods.

Exploring Geometry Using Hand-Held Games

The most exciting application of ARIS software, however, seems to be in its potential to create place-based, interactive, AR quests or games for hand-held devices along the lines of Pokemon GO. All of the pre-made ARIS games at the moment focus on Science concepts but I feel like there is interesting potential for Math instruction as well. Sinclair and Bruce (2015) discuss the value of engaging primary school aged children in more geometry using technology. As I was exploring the ARIS teacher tutorial, I was immediately struck by the possibility of teachers designing geometry quests that required students to actually move around the school, yard, or neighbourhood on a geometry scavenger hunt or even move following certain paths in the space in search of QR codes. Sinclair and Bruce (2015) share that “studied in North America have shown that geometry receives the least attention of the mathematical strands” (p.319). By grounding it in place-based, mobile TELEs teachers can weave geometric discussions into other strands of Mathematics such as numeracy and data management simply by making connections to the game. In addition, Sinclair and Bruce (2015) note the need extend “primary school geometry from its typical passive emphasis on vocabulary…to a more active meaning-making orientation…(including composing/decomposing, classifying, mapping and orienting,,,)” (p.32). Using ARIS to create activities around the school yard such as mapping all the right angles or using the satellite map feature to decompose the shapes of the school’s roof into composite shapes that can be classified allows students to visualize this kind of mathematical information in novel and engaging ways that take mathematics out of the textbook and into the real world. These endeavours correspond with the definition of Caleb Gattegno’s definition of the strand which Sinclair and Brown (2015) share: “Geometry is an awareness of imagery” (p.321).

In both these applications of Info-Vis software the teacher’s role would be to introduce the technology, create or aid in logging on and in, and perhaps provide some basic tutorials, and aid in the inevitable troubleshooting. Where ARIS for Mathematics is concerned, teachers would also be responsible for creating the augmented reality interactive stories that guide students in their math adventures. It’s important that teachers have a mature understanding of Content Knowledge for their target grade and particular class as they are designing these activities. Srinivasan et al. (2006) discusses “one aspect of motivation…goal challenge” which is explained as: “If learning goals are too steep for a learner’s current context, learning is not successful. On the other hand, when material is simple for the learner, the instruction can…lead to diminished performance…Thus, the task must present an optimal learning challenge…When this type of task is presented, students will perceive themselves as competent enough to be successful and enticed enough by the learning task to sustain their attention” (p.139). The students’ roles would be to interact with the software, reading, trying, re-reading, collaborating with their peers, and recording their findings or reporting back in whatever manner the activities warrant, hopefully within or through the technology that students are becoming familiar with as they interact with the content and each other within the game.

References

Bujak, K. R., Radu, I., Catrambone, R., MacIntyre, B., Zheng, R., & Golubski, G. (2013). A psychological perspective on augmented reality in the mathematics classroom. Computers & Education, 68, 536-544

Sinclair, N., & Bruce, C. D. (2015). New opportunities in geometry education at the primary school. ZDM, 47(3), 319-329.

Srinivasan, S., Perez, L. C., Palmer,R., Brooks,D., Wilson,K., & Fowler. D. (2006). Reality versus simulation. Journal of Science Education and Technology, 15(2), 137-141.

Reed Stevens (2012) The Missing Bodies of Mathematical Thinking and Learning Have Been Found, Journal of the Learning Sciences, 21(2), 337-346.

Winn, W. (2003). Learning in artificial environments: Embodiment, embeddedness, and dynamic adaptation. Technology, Instruction, Cognition and Learning, 1(1), 87-114.

E2A, Not Your Grandma’s Constructivism

Winn (2003) introduces a new “conceptual framework for studying learning in artificial environments” (abstract), which I’ve dubbed E2A, standing for Embodiment, Embeddedness, and Adaptation. These three concepts, he proposes, are to be taken holistically and provide a theoretical framework for considering how learning occurs from the perspective of cognitive neuroscience and systems theory. E2A considers how to explain how learning occurs when students work with “complex, computer-supported simulations of natural environments, referred to as ‘artificial environments’” (Winn, 2003, abstract).

Winn (2003) creates deliberate distance between E2A and several key aspects of constructivism. When educational researchers moved away from a computational view of learning, most sought answers through studying the contexts of learning under the umbrellas of “situated cognition” and “constructivism” but others began to study the act of learning as a result of adaptations between students and their environment which they viewed as a kind of complex system, thus applying principles of “systems theory” in their explanation of how the human mind learns. These educators turned to explanations for cognition related to the neurosciences, stating that “explanations of learning and cognition can be reduced no further than those emerging from the cognitive neurosciences” regardless of how complex directly describing and analysing learning processes proves when taking this paradigm as the starting point (Winn, 2003, p.3). These researchers propose an alternative framework to constructivism “based on the assumption that learning occurs when people adapt to their environment” wherein the learner is both embedded and physically active (Winn, 2003, p.3). From this arises the claim that cognition can be thought of as an “embodied” as well as a “cerebral” activity. Proponents of E2A take issue not with constructivism’s epistemelogical premise, but with its conclusions, citing it leans “dangerously towards solipsism” (p.12). Thus, “we arrive at a description of learning that is quite different from accounts given by traditional cognitive psychology and constructivism…The framework brings together recent research and theory that extend the purview of cognitive activity from the brain, through the body, to the environment itself” (p.22). Although Winn (2003) and other E2A proponents agree with constructivists that “cognition activity depends on the context in which it takes place” (p.5), they locate the construction of mental models (referred to as mental representations) in the scientific actions within the brain, via cognitive neuroscience, rather than occurring without attempted explanation of the phenomena by constructivists.

The foundation for this conceptual framework is the proposed cementing of three, previously separate ideas, into one “completely interdependent” self-organizing system:

(1) Cognition is embodied in physical activity which is,

(2) Embedded in an environment specifically designed to create learning, but that

(3) Learning does not occur passively or merely mentally, rather learning is the result of the “adaptation of the learner to the environment and the environment to the learner” (Winn, 2003, abstract).

The Four Learning Models & TELEs in E2A

I was intrigued by the theory of embodied learning and, although it stands apart from the metaphysical conclusions of constructivism, I sought to connect it to those previous learning frameworks from Module B. The concept of the body as our first STEM manipulative is a compelling one but I believe this goes beyond the simple (yet very valuable) truth that moving parts of the body in gesture or moving around in a physical space to literally embody the concepts of an object in motion are excellent, and under-utilized, ways to help students gain a more comprehensive understanding of STEM concepts. This description is only one way in which learning can be understood as “embodied” (Winn, 2003, p.11).

The concept of environment, specifically the environment-of-perspective referred to by Winn (2003) as the Umwelt lends a powerful hand to the case for artificial environments in learning. It is here that I began to see the connections of E2A to the other learning frameworks. “Beyond scaffolding (Linn, 1995), we can now embed pedagogical strategies into the very fabric of the environment. Since learning arises from adaptation to the environment, it can be guided by the behavior of the environment itself” (Winn, year, p.23). E2A therefore, seems to take SKI through the affordances of the WISE TELE as its starting point and then build upon that so that the technology is not simply the skeleton of the knowledge building experiences but actually couples the student within the artificial environment until that Umwelt actually becomes those experiences. “Learning is considered to arise from the reciprocal interaction between external, embodied, activity and internal, cerebral, activity, the whole being embedded in the environment in which it occurs. Learning is no longer confined to what goes on in the brain” (Winn, 2003, p.22).

The role and value of artificial environments are elevated when adopting this theory because the concept of embedded embodiment as the medium through which cognition (aka thinking) occurs is constrained by the limitations of our physical bodies. “The bandwidth of the data we can detect in the environment is limited” in terms of what a human can experience of light and sound and scales of space and time (Winn, 2003, p.7). However, such limitations can be reduced by the advances of artificial environments used as simulations of our natural environment. “Artificial environments can use computer technology to create metaphorical representations in order to bring to students concepts and principles that normally lie outside the reach of direct experience” (p.7). Using artificial environments such as a TELE is desirable, therefore, for an E2A pedagogy of learning. Dealing with misconceptions to create truer learning, they suggest using similuations to so what practitioners of TGEM do, that is, “to persuade students to reject such misconceptions and scientifically accurate conceptions in their place” (p.16) by actively propelling students into their Zone of Proximal Development through the deliberately timed release of confirming and confounding examples. As an example of a TELE, he referenced a really interesting looking (Minecraft-esque) study prepared for a PhD dissertation by S.L. Gabert 2001 called Phase World of Water where the author designs a VR environment for college students to explore a 3D graph of state of matter changes: Students’ VR avatars move through the 3 axis which aids students in developing deeper understanding of temperature, pressure, and volume in changes of state.

Winn (2003) draws on Hedden’s work on computer game design strategies which references Lepper and Malone’s theory of motivation that proposes the deliberate “direction of attention [through] challenge, curiosity, and fantasy” creates a circumstance called “flow” which corresponds to the “engagement, immersion and enjoyment” characterized by coupling or “presence”. They claim that these strategies in cognitively-driven virtual environments, as opposed to affectively-driven gaming envorinments, promote challenge and curiousity but “do not encourage fantasy” (p.18) but I disagree. I believe that the use of narrative is actually a better description of “fantasy”, in that it is the deliberate creation of a sense of “story” whether the ability to envision a real or imaginary setting, Puget Sound or a game world, and use the imagination to place oneself within that setting that is part of the draw of the narrative, a compelling sense of “place and time”, as well as of “character” or “events”. Everything students are doing in Virtual Puget Sound relies on the fantasy narrative in that the students are embedded within an Umwelt designed to evoke inquiry that is not actually the external, real life, environment. This is fundamentally no different than the narrative that is utilized in the Jasper series wherein students are invited to participate.

Winn (2003) cites recent suggestions that the term “embedded” is too passive, suggesting the student is being passively carried along by changes in the environment and, at least where participation in an artificial environment is concerned, is more accurately described by the concepts of “coupling”, “presence”, and “flow” between the student and the Umwelt, as is deliberately done by video game designers who program for affective (emotional) connectedness keeping players “engaged with their products for extended periods of time” (p.14). When it comes to the ability to describe cognitive processes and learning therefore, passivity is counterproductive because “successful students are anything but passive”. If successful coupling of learner to Umwelt (which she likens to the interconnectedness one might experiences when trying to catch a hamster with a pair of tongs) occurs “students can learn in an artificial environment in the same way that they learn in the natural world — intuitively, constructively and actively” (p.14).

Unsurprisingly, virtual immersion (ie. through VR HUDs rather than desktop computer simulations) increases presence because it increases coupling and thus cognitive gains increase proportionally. “Exposure to an environment can lead to physical changes in the brain, resulting in heightened perceptual sensitivity, which leads a person to actually see things differently in the environment” and enables students to “make distinctions [among objects and phenomena in the environment] with more certainty” (p.18). Examples given in support of this include Inuit seeing differences in snow, chicken sexers, or professional beer tasters heightened perceptions. “We have seen that tight coupling between a student and a learning environment leads to change in both the student and the environment. Adaptation is mutual” (p.20).

Winn (2003) brings out a really powerful idea by Varela et al. (1991) that “all of cognition is ‘enactive'” in the sense that “the way we organize ideas directly reflects how we act in the world” suggesting a “view of cognition that is based, not on the idea that the mind is a mirror of the environment, but that cognition consists of the constant, reciprocal, interaction between the mind and the environment” (Winn, 2003, p.11, emphasis added). All in all, E2A is a very powerful vehicle for considering human cognition and I believe it has significant applications to guiding pedagogical choices for educators.

Questions

(1) In what other ways is E2A different from the constructivist epistemology we’ve studied in MET thus far?

(2) Which of the theories in Module B best fit within an E2A framework, in your opinion?

LfU, GIS, & Minecraft Club

Some Belated Thoughts on LfU & GIS

As with the WISE lesson, when this lesson asked that I suggest other STEM topics where LfU principles could be applied or how I might adapt it to Math I was stumped. As a rule, I do not like to read the posts of my peers before I have made my own ideas and contribution because I then feel unduly influenced or sometimes like I am taking their ideas rather than forming my own, so I relied on the readings and my own knowledge and in this circumstance that was not enough for me to successfully engage with this level of thinking.

However, I was very impressed with the use described in the Create a World project (Edelson, 2001) using the WorldWatcher (MyWorld) GIS. The relationship between landforms and climate is a fuzzy one for most students (myself included) and I wish I could have gone through such a unit myself in school. I also really liked how the LfU model demands that lessons are explicitly designed to target all three of their steps in the process of developing usable learning. The table was well-organized and allowed me to understand how the developers of Create a World structured the knowledge activities after this model. Now, as I reflect on these concepts I believe, as an educator, with some more exposure to this model and a refresher on the complex relationship concepts in Science curricula I could more easily visualize its applications to other topics within STEM. At the time of this module’s lesson I felt unqualified to suggest how else it might be used for learning STEM topics.

In preparation for my ePortfolio contribution for this lesson, I returned to my notes on the readings and the discussion activities on the blog. Now, I also notice that the Motivate, Construct, Refine process closely mirrors the principles of Generate, Modify, Evaluate. I also found I really liked Mary’s post about Grade 2 Social Studies applications using Google My Maps. I agree that the MyWorld GIS program is not necessarily primary-student-friendly and My Maps sounds like a much more feasible tool. I was also astounded to read in her comments that that one Social Studies expectation takes six months to cover! I wonder how many expectations Alberta has for Grade 2 Social Studies? Only two at that rate of coverage?? I wish I had been able to be present for this discussion during the time that the comments would be watched so I could ask Mary these things. I was impressed with the inquiry wording her province created, at first I thought she was listing a project she had created herself. Ontario does not have such targeted language where inquiry is concerned, to my knowledge (nor do we have textbooks for primary grades).

In what ways would you teach an LfU-based activity to explore a concept in math or science? Draw on LfU and My World scholarship to support your pedagogical directions. Given its social and cognitive affordances, extend the discussion by describing how the activity and roles of the teacher and students are aligned with LfU principles.

The notion that learning does not take place without the choice of the learner to understand, whether via conscious or unconscious “understanding goals”, as artiulated in LfU’s second principle — “knowledge construction is a goal-directed process that is guided by a combination of conscious and unconscious ‘understanding goals’” (Edelson, 2001, p.357, emphasis added), is very important as a foundation for the creation of curiosity which GEM, Jasper and WISE also acknowledge. The implication of this principle for the classroom is that “learning” must be (and can only be) initiated by the learner, whether it is through conscious goal-setting or as a natural, unconscious result of experience. This places the teacher’s role squarely in the realm of “experience facilitator” and it follows that useful structures of lesson creation to this end, such as what the LfU process tables are modelling, would be extremely valuable.

I had collected the following quote during my initial readings (emphasis added) and upon re-reading it I was finally able to make a connection that I felt satisfied the above question.

“The place-based educational approach uses the local environment to teach across the curriculum(Sobel, 2004). It emphasizes hands-on, real-world learning, which engages students and, by connecting the GIS unit with an ecology unit on succession, makes GIS acceptable to the teachers. By entering and querying data in the GIS, students worked with maps in a novel way that reinforced and improved their understanding of spatial relationships in their schoolyard. Based on these results, using a place-based approach seems a valuable way to teach students GIS. Introducing GIS and GPS in the students’ familiar and immediate surroundings more easily bridges the gap between the real and digital worlds…Using a place-based approach is inherently more interesting to students than using a generic, one-size-fits-all data set, and the results demonstrate that using GIS as a classroom tool can effectively develop students’ spatial awareness while they learn more traditional topics in ecology” (Perkins, Hazelton, Erickson, & Allan, 2010, p.217).

I feel like the above bolded and underlined quote can apply to Math as well. In general, if we use place-based data sets (perhaps even student collected) rather than textbook-provided examples students can more easily connect to concepts of number and size and distance. Finding the area of our classrooms rather than the iamginary spaces listed in the text would be one example. This got me thinking about the activities we are undertaking in our Minecraft STEM Club this year. I believe the idea of place-based LfU can be applied with a TELE such as Minecraft Education Edition. We are currently beginning the process of measuring our school building in order to graph it and build it MCEE with a recently revised scale of 1 metre = 2 blocks. Reading this quote after reading Mary’s post (linked above) caused me to wonder if perhaps a GIS like Google Earth can show us the school building and yard and then we can import that into Google My Maps to calculate distances for the perimeter of the build? We can then compare that data with the trundle-wheel walking measurements we’ve been taking to inform our grid paper drawings which we will draw in our scale to guide our builders in Minecraft.

The students are the ones doing the measuring, graphing and building. As the teacher, my role is to provide the structure for their explorations. For example, as we continued to measure different rooms’ lengths and widths some students were able to estimate the height of the ceiling and then check with the secretary and custodian about the actual heights. We discovered that some ceilings were only about 2.5 m high. I then asked them how they felt about our original scale for this project which had been 1 metre = 1 block. They decided that such a scale would be too small where the height of the rooms was concerned. A good discussion about whether we can just change the scale for the height axis or whether that wouldn’t be consistent with the concept of a model being “to scale” ensued. They wondered whether the new scale would make the lengths and widths of the room appear exceptionally large in-game. Finally, the students decided that we should alter the complete scale, and our previous grid paper drawings, to reflect their new knowledge so that the scale of every axis for our build would now be 1 metre = 2 blocks. Although I did not plan this using an LfU table, in retrospect and looking ahead, I can see how these discussions fall into the Motivate, Construct, and Refine processes of learning.

References

Edelson, D.C. (2001). Learning-for-use: A framework for the design of technology-supported inquiry activities. Journal of Research in Science Teaching,38(3), 355-385. Retrieved from http://ezproxy.library.ubc.ca/login?url=http://dx.doi.org/ 10.1002/1098-2736(200103)38:3<355::aid-tea1010>3.0.CO;2-M

Perkins, N., Hazelton, E., Erickson, J., & Allan, W. (2010). Place-based education and geographic information systems: Enhancing the spatial awareness of middle school students in Maine. Journal of Geography, 109(5), 213-218. Retrieved from https://www-tandfonline-com.ezproxy.library.ubc.ca/doi/abs/10.1080/00221341.2010.501457

SKI/WISE and Primary Students

On The Task of Modifying an Existing WISE Lesson to Share During Module B…

I was unable to contribute this post within the course deadline for discourse. I found this particular portion of Module B overwhelming in terms of the amount of readings and questions that we were asked to engage with. This, coupled with several compounding crisis in my personal life, severely limited my ability to interact with my peers during the rest of Module B and the beginning of Module C. Where WISE in particular is concerned, I did not truly understand what WISE was until engaging with Kari and David’s comments from the TELE Synthesis Forum (B4.2, see Take Aways under the Home tab for these comments). It wasn’t until then that I saw that WISE was not a learning framework in and of itself but was actually a technology-enhanced design tool (a technology scaffold, if you will) allowing teachers to create guided-inquiry lessons for students using web- or tech-based tools, or better yet allowing actual, specific kinds of inquiry learning frameworks to guide their lesson designs.

When previewing the WISE “What Makes a Good Cancer Medicine” lesson I enjoyed how they jumped right into sequencing which types of cells experienced mitosis the fastest without any pre-teaching about them, requiring students to use their prior knowledge without help. Then the feedback for incorrect answers gave hints on how to access more specific schema but didn’t tell the answers. Very rewarding and I learned things I didn’t know already! And then the prediction part didn’t give me immediate feedback and I knew that I didn’t know whether my answers were correct so I was actively looking in the next sections to see if I could find the answers, kind of like a game or a quest. This really increased my motivation to search and keep reading. At the conclusion of the lesson, however, I still feel like I hadn’t found the feedback I needed to know to identify the correct answers and I was disappointed that the project hadn’t fulfilled the expectations for my understanding that it had set me up for.

When this lesson’s task asked us to modify a WISE project for our contexts I found this extremely difficult because I am not a STEM teacher and am mostly a primary (1-3) grade teacher, for which WISE offers no projects (when grade filters are engaged in their Project Library). I explored a few projects, such as the middle school Music one, but found it too large a task to modify for my Grade 3 music students because it was so focused on the Science and I only teach the Music component to them, sound is not in their Science curriculum for several more years. My favourite WISE project was one of the iterations of “Graphs Tell a Story”. There, I found lessons that followed a logical sequence and allowed me, as the student, to truly understand how a graph could be used to tell a motion story. I really enjoyed working with the swimming animation to chart the graph and then see if I was right based on whether the animation moved properly. Again, however, I was at a loss about how to modify this project in any meaningful way. For these reasons I felt unable to share anything of substance that adequately met the requirements of this module’s lesson.

If I had understood then what I did later after Kari’s synthesis post, perhaps things would have been different, but actually I might not have been able to attempt this lesson creation yet anyway because I had not experienced the most significant TELE for me, TGEM. In my opinion, I would have liked to have had it explicitly explained that WISE was a framework program, and have this separated from the very heavy use of theory explaining SKI and the admirable creation and maintenance of the WISE Project Library. Then, I would wish WISE to be the last lesson in this module so that I could have attempted to create a new project using WISE and incorporating elements of Anchored Instruction/Place-Based LfU, GEM cycles, and SKI all within a WISE project “learning portal” so to speak. Although I acknowledge the bias of hindsight, I feel that those changes in instructional delivery would have allowed me to feel less overwhelmed and to be more successful in reaching this module’s learning goals.

I really appreciate this ePortfolio assignment because it allowed me to go back and revisit these topics which I had found confusing and finally make the connections I need to feel like I have a solid understanding. If I had to choose a WISE project to modify, I would have chosen the “Graphs Tell a Story” and worked to modify the content to be primary-student-friendly as they worked in a unit on reading, designing and interpreting line graphs. Alternatively, using the WISE TELE to revitalize Jasper’s relevance in today’s technology would be an excellent application of this tool. For example, the Rescue At Boone’s Meadow could be run using appropriate SKI patterns with ease.

Now I see that a WISE project is a powerful tool indeed, particularly for STEM teachers, but also for non-STEM teachers desiring to create model-based reasoning with inquiry patterns in a technology enhanced environment for literate students. I am not certain primary aged students or those who struggle with reading would be able to find success within a WISE project, but for those who read and are relatively competent in self-direction, learning through WISE seems ideal in many ways. Lack of technology continues to be a constraint, as does time to create or revise a project to meet unique contexts, but if a ready-made project which made it to the Project Library fit a class’ needs this would be a wonderful learning tool which could be co-taught in the homeroom/rotary classroom as well as the Library.

Revisiting Grade 3 Buoyancy Misconceptions Using TGEM & PhET

As I was reading the instructions for this post I decided to remix one of my earlier ideas (which I had posted so late passed the deadline I missed the chance at peer interaction) because it fit so well into this assignment (and I was proud of it and wanted it to have another chance at generating conversation!) 😉

I chose to focus on the TGEM framework and utilized a PhET applet. The misconception I selected was that of buoyancy and its relationship with gravity/mass/density. As I pointed out in the first iteration: In Grade 3, students in Ontario study material forces. I recall classes having a hard time understanding why the buoyant force allowed certain objects to seemingly overcome the force of gravity but not others. The concepts of mass, volume, and density are not solidified at this stage so explanations or even demonstrations were not usually deeply understood. There are several buoyancy simulations available online but I feel the PhET one described below is the most useful. As Finkelstein et al. (2005) mention PhET simulations “are designed to be highly interactive, engaging, and…provide animated feedback to the user. The simulations model physically accurate, highly visual, dynamic representations of physics principles” (p.2). Furthermore, this particular Info-Vis simulations also provides a ready-made set of data (which I considered “large” for the purposes of primary education) required within the GEM framework that the students could refer back to as they gained deeper understanding of what they were looking at (Khan, 2007).

If I had an opportunity to teach this Science unit again using T-GEM cycles and Info-Vis applets the lesson activities might look something like this (over a series of classes, I’m sure)…

Buoyancy & Mass Lessons ala TGEM & PhET

Step 1: Compile Information – I would begin with showing students a data table for five blocks of mystery objects from the PhEt Density & Buoyancy Simulation and demonstrating how to read a two-column chart. Then we would briefly discuss what students know about these objects, the abbreviations (what does L and kg stand for?) and the numbers beside them (making a connection to money when reading decimals, are these numbers placed in any particular order?). Add keywords to a word wall: litres (L), kilograms (kg).

Source: https://phet.colorado.edu/sims/density-and-buoyancy/density_en.html

Step 2: GEM Cycle 1

Generate – Then, I would begin by asking students to find trends or generate some relationship statements about the data in groups and share with the class. For example, “The water has the smallest number but the gold has the largest number” or “I wonder why gasoline is smaller than water? Aren’t they both liquids?” Other questions related to the nature of the data the teacher might guide discussions of include: “What might ‘density’ be measuring?”, “Why is the pool measured as 100 L but the scale measuring 0 kg right now?”

Then, I would direct their attention to the cubes and ask them to explain what they see: Each shape is a cube, they’re five different sizes, five different colours, labelled with five different letters. I would ask them to put the cubes in order in two ways (letter label and size) and then to predict what the scale would read if I were to measure each cube. (I would deliberately not use the term “weigh” or introduce the term “mass” at this point). I would also ask them to predict whether they think any of the numbers on the data table might appear on the kg scale and whether/how the 100 L measurement of the pool might change.

Then, I would ask students to predict which cube would measure the highest number when I place it on the kilogram scale. (They will likely say the largest cube will be highest and smallest lowest and I will add the word “size” to our word wall). I would ask them to write a rule explaining what they think the relationship between a cube’s size and its kilogram measurement.

Evaluate – Now, I would begin the simulation by placing each cube on the scale and have a student scribe for the class to record the data in a new table:

Block Label	Size (1-5, 5=largest)	KiloGrams (kg)

I’m deliberately constraining them at this point by doing this part of the simulation as a demonstration to keep them from dropping the blocks into the pool or changing any of the other variables. I’d ask them to reflect on what they saw: Were your predictions completely correct? How can you explain this? I’d ask them to notice the L measurement change and compare that by measuring the block on the kg scale again and compare these numbers…

Modify – Finally, I’d ask the students if their original rule needs to be changed now that they’ve seen the measurements. Then I’d have their groups try to make a new rule explaining why each block received the measurement it did since now they see that it can’t be because of its size.

Step 3: GEM Cycle 2

Generate – To start the second cycle, I would ask students to predict what will happen when each block is dropped into the pool and explain their thinking. If they say the same thing will happen to all five blocks (ie. all sink or all float) I would not correct that at this point. I would ask them to draw what would happen on a two-column drawing one side for “prediction” the other for “actual”. I’d again ask them in their groups to write a “rule” for predicting what will happen to a block when it’s dropped into a pool of water.

Evaluate – Now, the students would stay in their groups and load the simulation themselves using the Mystery button and experimenting with dropping the blocks into the water, and drawing what actually happened beside their predictions. I’d ask them to reflect on what they saw: Were your predictions completely correct? How can you explain this?

Modify – I’d again ask the students if this original rule needs to be changed now that they’ve run the simulation and have their groups try to make a new rule explaining why each block behaved as it did when dropped into the pool and write that down. I’d ask them to record the kg of each block on the “actual” side of their diagrams and consider whether this number might be connected to what they observed in the simulation or not when they make their new rule…?

Step 4: GEM Cycle 3

Generate – At this point, I would ask students to predict what will happen when each block is dropped into the pool if the simulation is changed so that all blocks have at least one thing the same, if they all measured the same kilograms for example. I’d again ask them in their groups to write three “rules” for predicting what will happen to the blocks that are all the same (a) mass, (b) volume, and (c) density when they’re dropped into a pool of water (it’s not important that they don’t know what these terms mean, this is part of the discovery).

Evaluate – Then, the students would stay in their groups and load the simulation themselves and use the “same” x buttons to set the blocks to the same value and continue experimenting with dropping the blocks into the water. I’d ask them to reflect on what they saw and evaluate their predicted rules. I’d assign a role to one of the group members to keep a running record of “things we want to know/don’t understand” and to another as the recorder to write or draw the group predictions and rules and the actual results. At the conclusion of this part of the simulations, I’d ask them to come up with a working definition of the terms “mass”, “volume”, and density” that they’ve been observing.

Modify – I’d again ask the students if their original rules needed to be changed now that they’ve run the simulations and have their groups try to make new rules explaining why each block behaved as it did. I’d challenge them to incorporate their definitions of “mass” and “density” into their explanations.

Step 5: GEM Cycle 4

Generate – Finally, I would ask students to think about four materials that come in blocks they are familiar with: Ice, Metal, Wood, and Styrofoam. I would ask them to explain to me what would happen if I threw a block with the same mass but of each different material into the pool. (I might bring in these objects and a bowl or aquarium to help them imagine). I would then return to the Mystery simulation screen and reveal to them that the blocks in this simulation are each made of a different mystery material just like my example objects. I would ask them to generate a rule using material names for what would happen when we dropped those materials into a pool.

Evaluate – So now, the students would stay in their groups and load the simulation but go to the Custom button. I’d ask them to experiment with the different materials, their masses and volumes and explore/record/discuss what happens.

Modify – I’d ask the groups to use this information to try to identify the material of each mystery block using the data from all the simulation tabs. As an extension, I’d introduce the Buoyancy Simulation (Intro tab only) and allow them to gather information to inform their hypothesis from those materials and we’d discuss the concept of weight (N) versus mass (kg) at this point, while formally introducing the topic of the buoyant force. Finally, we’d return to the data table from the first cycle and ask students to explain what it means that wood has a density of 0.40 kg/L while lead and gold (both metals) have a much higher density. What would happen when we drop wood into the pool versus metal? Then in the Buoyancy Playground tab of that simulation, they’d compare materials such as styrofoam, wood, or metal and craft two final truth statements (1) about gravity (N or kg) and density, (2) about density and buoyancy.

Step 6: Consolidation and Extension/Next Steps

I’d ask the groups to tweak their truth statements until they feel ready to share them with other groups, then write them on a chart paper, leaving the marker there, and go do a gallery walk to see what other groups decided. Viewers can record their affirmative or contradictory ideas and questions underneath the truth statements, from “Yes, we agree” to “What about … ?” or “But x doesn’t y so how do you explain that?” Groups would then come back together to read and reflect on the feedback, going back into the visualizations and revising their ideas as necessary. I’d have them hand in a paper copy of their two finalized statements for formative assessment.

Finally, I’d draw their attention to the bottom of both tabs in the Buoyancy Simulations where the density of the fluid within the pool can be changed and observe what happens to the blocks when the fluid is converted to “air” “gasoline” “olive oil” “water” or “honey”. A conversation about viscosity is beyond the Grade 3 curriculum but students with Gifted designations would still be able to grasp that, if not the rest of the students, especially when presented using this format.

Synthesis

Finkelstein et al. (2005) points out that “it is possible, and in the right conditions preferable, to substitute virtual equipment for real laboratory equipment” (p.6) and in this circumstance I completely agree. In the past, I have attempted to teach concepts of mass, density and the buoyant force using an actual aquarium filled with water and a variety of real objects. There was not enough equipment to go around, a lot of watching the pushier kids do it, a lot of mess to clean up, noise to contain (I teach in an open concept building where this is an issue) and frankly, very little real learning other than comments about “how cool” that was. This simulation, particularly planned using the TGEM framework, would have accomplished real learning goals in a much more satisfying, comprehensive, and inclusive manner. Combining the TGEM framework with PhET also addresses the issue Yeo et al. (in Finkelstein, 2005) noted that timely “reflective points” should be provided to ensure students can’t just “exit a screen with alternative concepts left intact” (p.6).

It’s interesting to note the findings of Srinivassan et al. (2006) that students learning via a simulation “don’t have a sense of partaking in what they perceive as authentic experience[s]. They seem to need/want authenticity to be able to make the connections the experts make with the simulations” [i.e. that the results of the simulation are the same as if they are using “real” items] (p.140). I wonder if my students would feel the same way? Would they be able to transfer their truth statements from the simulations above to real life problems, accurately predicting where a cube of a particular material would float in a real aquarium for example?

Admittedly, such lessons, even without the extensions, would take quite a bit of class time to navigate successfully and that is always a serious drawback in the real world of teaching. Nevertheless, when it comes to applying this to my (previous) practice, visualizing information, and applying a learning framework specifically to address a misconception, I believe it would extremely effective compared to what I’ve done in the past. Who knows, I might even see if the Grade 3 teacher would like to collaborate and run this lesson during our Library/Tech periods! 😉

Discussion

Have you taught these concepts in a different way or to a different age group? Are you familiar with some of the other buoyancy-esque online tools, such as BBCs InfoBits or YouTube videos, and how do you think they compare?
Do you think there’s a way to accomplish the learning goal while keeping the TGEM and Info-Vis lesson models without sacrificing so much class time?
What about summative assessment? In my opinion, it feels wrong to assess knowledge gained using simulations, visualizations, and the scientific equivalent of what Sinclair and Bruce (2015) refer to as virtual manipulatives with a pencil and paper activity/test. Can you suggest a more integrous way to assess student learning at the conclusion of this?

References

Finkelstein, N.D., Perkins, K.K., Adams, W., Kohl, P., & Podolefsky, N. (2005). When learning about the real world is better done virtually: A study of substituting computer simulations for laboratory equipment. Physics Education Research,1(1), 1-8.

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Sinclair, N., & Bruce, C. D. (2015). New opportunities in geometry education at the primary school. ZDM, 47(3), 319-329.

Srinivasan, S., Perez, L. C., Palmer,R., Brooks,D., Wilson,K., & Fowler. D. (2006). Reality versus simulation. Journal of Science Education and Technology, 15(2), 137-141.

Are Formal Learning Systems Failing to Achieve TRUE Knowledge Construction?

How is knowledge relevant to math or science constructed? How is it possibly generated in these networked communities? Provide examples to illustrate your points.

Mathematical knowledge is constructed by reason of use in relevant circumstances which may or may not occur within a formal classroom setting as shown by Carraher, Carraher, and Schliemann (1985). They found that the Brazilian children working as street vendors were able to perform mathematical computations, always without the use of paper and pencil and often above their equivalent formal “grade level”. This learning was anchored directly to their authentic contexts and not easily transferred into a school mathematics environment, however. These same children were not able to perform similar computations when presented with “formal mathematical problems without context and…word problems referring to imaginary situations” (p.24) that nevertheless used the same numbers or items they were able to compute in the informal setting. The mitigating factor appears to be that formal mathematics requires students to take contextualized situations (ie. the real life “word problems” of a customer asking them about the price of a certain quantity of coconuts) and translate them into algebraic expressions. The perceived deficit in mathematical knowledge found in the formal assessment is not about the child’s ability to compute values correctly at all, but is, in fact, about her “expertise in manipulating symbols” (p.25).

Networked communities, whether formal school classrooms, interactive museum exhibits, or virtual field trips can aid in this generation of knowledge by contextualizing concepts in authentic and relevant phenomena. Carraher, Carraher, and Schliemann (1985) suggest “seek[ing] ways of introducing these systems [of thinking] in contexts which allow them to be sustained by human daily sense” (p.28). Such a thing does not happen by accident, as Moss (2003) points out in his critique of one implementation of the JASON project. Even when professional development and classroom implementation is available, truly connective communities of practice that result in long-term retention of scientific concepts and reforming student understanding of the nature of science through formal settings is not guaranteed. Moss’s (2003) observations of science learning supports the previous authors observations of mathematical learning when he states that “students’ conception often can develop in the home and community, and do not necessarily develop in classrooms. It is essential that we recognize that learning science occurs beyond the science classroom throughout many aspects of students’ lives, and it is critical that we facilitate learning opportunities in class which take these prior experiences into account” (p.24). These networks, when leveraged properly, have the potential to provide authentic science and math experiences that may help bridge the gap between informal, generative knowledge that’s grounded in relevant contexts and is retained, and the formal algorithms and facts that must be translated into symbol-systems and manipulated in the short-term to demonstrate “learning” at school.

Discussion:

Moss (2003) suggests that Student Scientist Partnerships “must be viewed as complementary, and even beneficial, to testing initiatives which are driving the choice of curricular programs” (p.29) but that the way teacher training was handled and the constraint of time contributed to an ineffective implementation of the JASON project to that end. How might teachers or schools ensure that time invested in interactive and virtual learning has longer-lasting, richer effects than simply getting students to feel excited for the duration of the project?

References

Carraher, T. N., Carraher, D. W., & Schliemann, A. D. (1985). Mathematics in the streets and in schools. British journal of developmental psychology, 3(1), 21-29.

Moss, D.M. (2003). A window on science: Exploring the JASON Project and student conceptions of science. Journal of Science Education and Technology, 12(1), 21-30.

Jasper and T-Gem and WISE, oh my!

The four learning theories we explored in Module B have many similarities among and between themselves. All four theories (Anchored Instruction, Scaffolded Knowledge Integration, Learning-for-Use, and Generate-Evaluate-Modify) are founded in constructivist pedagogy, particularly in the way student knowledge is created and how teachers need to design learning experiences if they really believe this to be true. All four theories are concerned with student motivation, curiosity, and reflection in order for true learning to occur. All believe that an authentic context to some degree or another must be used to anchor student explorations and subsequent evaluations of hypothesis/explanations. All promote the teacher as a facilitator who is not the primary source for disseminating knowledge and who deliberately withholds pertinent information along the way, releasing it only after students have become engaged in the problem, have realized they need the information, or have proven unable to generate the information among themselves. Problem-finding and problem-solving are valued, and confusion or even frustration when confronted with outlier cases or unknown formulas/information is embraced as a fundamental prerequisite for generative learning.

A Graphic Comparison

I created a graphic organizer to sort my thoughts when comparing and contrasting other aspects of these TELEs:

Synthesis

From the exploration of the above learning theories, I’ve learned that technology use for education, whether STEM or other subjects, should be deliberate and purposeful. Teachers should become aware of well-designed technology-enhanced spaces, such as WISE projects and PhET simulations, or design/modify their own TELEs to meet learning needs based on their own foundational pedagogical beliefs. Constructivist theories can be well-served using TELEs when teachers invest time initially to reflect, research, and plan how best to integrate the tenants of constructivism (student-centered, teacher-facilitated, curiosity-driven, and collaboration-based explorations and reflections) using technological tools. Simulations, visualizations and large data-sets are excellent tools for generating curiosity and recursive, adaptive feedback, as well as for promoting social learning through generative discussions, explorations, evaluations and explanations of mental models. Narrative structures and place-based learning also encourage learners to become more motivated to find problems and evaluate their own solutions because real-world, authentic contexts make STEM ideas visible and therefore more relevant. Inquiry-based learning does not always have to mean messy experiments, maker-spaces, or individual research projects; the foundations of inquiry (curiosity, needs-driven knowledge seeking, and communication) can be accomplished through classroom structured lessons rather than only in laboratory contexts. These learning theories and their related TELEs did a great job of articulating in a practical way how teachers desiring a more constructivist pedagogical approach can actually promote and maintain students positions in their Zones of Proximal Development by showing that pre-teaching content before asking them to solve problems using that knowledge is not necessary and perhaps even counter-productive to the process of inquiry needed to reduce the development of “inert knowledge” and promote the development of “generative learning”.