Author Archives: scott skanes

Constructive Debates or: The Importance of Not Keeping Thinking Private

How is knowledge relevant to math or science constructed? How is it possibly generated in these networked communities? Provide examples to illustrate your points.

Morally Scientific

Lampert (1990) sought to change “the meaning of knowing and learning” in school by initiating and supporting social interactions appropriate to making mathematical arguments in response to students’ conjectures. Her aim was to give up conventional academic interaction, instead while seeking to help students act with “the moral qualities of a scientist” (p. 58). She compared the process, quite elegantly, to dancing, stating that it ““required some telling, some showing, some doing it with them along with regular rehearsals” (p. 58).

Perhaps the crux of her approach was an emphasis on avoidance of silence, and of a traditionally top-down approach to mathematics “learning”. She noted the importance of not keeping thinking implicit or private, suggesting that mathematics often involves “arguing, defending, challenging, and providing one’s own ideas” (p. 56).

The Great Divide

I really appreciated how Lampert described the inconsistency of how math is approached in and out of the classroom. In “real life” mathematical and scientific ideas are questioned almost constantly, and often hotly debated, and uncertainty on all sides is expected as a natural component of the process. Sometimes, the “right answer” may not even exist, or if it does it could be nearly impossible to prove. Unfortunately, “classroom” mathematics is too often entirely void of this essential process of questioning, these heated debates, and this exciting layer of uncertainty hovering over the proceedings. Instead, mathematics teaching encourages a flow of knowledge from top-to-bottom, with the “best” teachers often considered the ones who help students achieve the highest marks in the most efficient number of steps. What a wasted opportunity for learning.

Lampart took several approaches to counteract this stagnant learning environment:

Providing students with open-ended problems to solve
Collecting student responses and having them explain why another student’s answer is incorrect, or explain why they believe those answers to be correct
Engaging in “cross-country” mathematics

This last point, “cross-country” mathematics, suggests that the problem-solving terrain” is “jagged and uncertain” (p. 41), and that watching someone traverse it (be it a teacher or even another student) is a key to learning how to traverse that terrain themselves. To be more specific, if it is only the teacher clearly demonstrating the rules, students will only see a limited picture of what’s necessary for expertise in the area, and will not learn how to solve anything but the most straightforward problems, and only in one standard way (p. 42).

The Right Stuff

Lampert found that by essentially refusing to give “the right answer”, students were forced to search for solutions to their problems in more creative and collaborative ways, often leading them to discuss with each other. Over time, students assumed the role of more experienced “knowers”, and became more comfortable and competent in mathematical discourse and, better embodying “the moral qualities of a scientist”.

Knowledge Construction

Lampert’s work, although probably not as extensive or rigorous as some of the other papers I’ve encountered, does point to the importance of students being co-constructors of knowledge. Her report suggests that knowledge relevant to math (and science) is perhaps best constructed constant questioning and debate. This approach allows all aspects of a problem to be explored, for all students to be involved in the generating of an answer (even in the absence of an all-knowing sage-like answer-distributing teacher) while ensuring that the answer to any given problem is the result of a collaborative effort from “all” students. Note: I say “all” because, without some help and encouragement from teachers, some students may be extremely unwilling to “put themselves out there” in a classroom debate.

A GLOBE-al Network

This week, I explored GLOBE.

Aside: I was impressed that a program that was first formed in 1995 has had continuous development work done on it, which is clear in its modern website’s presentation. I also had a literal “LOL” at David Dykstra’s comment about WhaleNet, which acts as a nice reminder that websites from the 90’s don’t get modernized by themselves.

Networked communities like GLOBE are not dissimilar from the above approach to math and science learning: GLOBE takes a “cross country” approach in its lack of a well-marked path, and its emphasis on exploration and discussion without a clear “right answer”. Students are literally acting not just with the “moral qualities” of scientists, but literal scientists, as they collect a variety of data in a standardized way. Sure, the structure of the program is slightly constricting, but the rigidly-structured data collection allows for their results to be compared, discussed, and debated with an online community without the fear of having their data thrown out due to invalid collection technique. Plus, standardized approaches to data collection does not negate opportunity for scientific discovery or discourse. I enjoy how GLOBE invites students (and their teachers) to take a trek into the unknown as they collect real-life data based on their own contexts, then get to compare said data with thousands of other students worldwide.

Clear Direction… to a Fault?

I do wonder, however, how effective GLOBE might be for developing critical/independent thinking skills. While the data collection and community aspects can allow for discovery and engagement, the GLOBE lessons provided for teachers seem highly scaffolded, including very specific instructions and assessment methods. What do you think… do specific instructions for teachers risk detracting from the exploratory essence of the program? Do you think greater teacher with GLOBE could result in a more genuine experience which expects more from students in terms of generative learning?

Thanks for reading 🙂

Scott

References

Butler, D. M., & MacGregor, I. D. (2003). GLOBE: Science and education. Journal of Geoscience Education, 51(1), 9-20.

Lampert, M. (1990). When the problem is not the question and the solution is not the answer: Mathematical knowing and teaching. American Educational Research Journal, 27(1), 29-63.

Physicality in a Virtual World?

Cognitive Learning Theory Renaissance

I found this week’s readings to be quite engaging as it was mostly new information for me. I mean, I’ve always felt that there was a clear benefit to having students physically engage with content in order to solidify their learning, but I’ve never had it explained to me in the detailed and justified way it was explained by Winn (2003). I learned that cognitive learning theories were strayed away from for some time, to be essentially replaced by constructivist and social learning theory approaches. Their downside seemed to be how they segregated the brain’s “internal, cerebral activity” (Winn, 2003) from the immediate environment.

Well, it turns out that learning is inextricably linked our internal, cerebral activities are to external, “embodied” activities; two seeming-opposites engaged in an endless, reciprocal dance named “dynamic adaptation” resulting in learning. These concepts are what engaged me; to consider learning as not only the result of internally-generated knowledge structures but to be described as a series of “distinctions”, environmentally-triggered, which pressure us to adapt. Perhaps even more fascinating is the rabbit hole that opens once you start to consider learning as being fundamentally linked to environment. This means that everyone’s learning, or perceived world, is literally unique, shaped by their environment and naturally-varied experiences as well as genetics, while being constrained by sensory limitations (all essentially related to the concept of “Umwelt”).

Environment guides Learning

What I found perhaps most impressive about Winn’s writing was the clarity in the explanations of how how learning can be guided by the environment itself. There are four stages:

Declare a Break
- Activity is somehow interrupted by noticing something new or unaccounted for
Draw a Distinction
- Sorting the new from the familiar
Ground the Distinction
- Integrate the new distinction into the existing knowledge network (or, if it defies deeply-rooted beliefs, it will simply be memorized then forgotten – sound familiar??)
Embody the Distinction
- The new distinction is applied to solve a problem

Artificial environments (e.g. video games, VR) can allow us to go beyond scaffolding (such as seen in SKI/WISE) and embed pedagogical strategies into the environment itself by understanding these four stages. I mean, why not? Rarely can we design every aspect of our real-world environments, but we certainly can in video games and VR experiences. Of course, not everyone is a game designer, but most of us could manage to create a Virtual Field Trip, for example. The experiences could be designed so that they force students to create a “series of new distinctions” which could lead them to understanding whole environments (Winn, 2003); something extremely powerful especially for students that could never visit the environment in person.

A Variety of Applications

I think that even topics like quadratic equations and parabolas could benefit from this embodied earning approach. This could look like anything from a teacher designing a “tactile” activity in Activity Builder on Desmos, or leveraging tools like those found on GeoGebra or NCTM (e.g. sliders, tap-and-drag functionalities) for a more interactive, embodied experience. Tech allows us to explore abstract concepts in an embodied way, which is perhaps one of its greatest affordances.

Affordances of VLEs

All this thinking led me to explore more recent papers on the subject of virtual environments. It turns out significant research has been done on VLEs (Virtual Learning Environments). For example, I came across a paper by Dalgarno and Lee’s (2010) that identified five affordances (or benefits) of VLEs that translate directly into learning benefits:

spatial knowledge representation,
experiential learning,
engagement,
contextual learning, and
collaborative learning.

These probably come as little to no surprise to most of us, but it is certainly nice to have them listed so simply and to know that significant research has determined their effectiveness.

VLE’s Unique Characteristics

Dalgarno and Lee’s work also argued that 3D VLEs have two unique characteristics, “representational fidelity” and “learner interaction”, both of which I feel are particularly essential to both video games and VR design.

Unique Characteristics of 3D VLEs
Representational Fidelity	Learner Interaction
Realistic display of environment Smooth display of view changes and object motion (e.g. high frame rate) Consistency of object behaviour (e.g. realistic physics) User representation (e.g. avatars) Spatial audio (e.g. 7.1 surround) Kinesthetic and tactile force feedback (e.g. rumble functionality)	Embodied actions (e.g. physical manipulatives in a virtual environment) Embodied verbal and non-communications (e.g. chat functionality, online/local multiplay) Control of environmental attributes and behaviour (e.g. customization interface) Construction/scripting of objects and behaviours (e.g. programmed functionalities are possible and at the whim of the programmer/designer)

(all examples in brackets above are my own contributions)

Basically, when these two characteristics mingle, deeper learning experiences are bound to take place as they leverage the five affordances that translate directly into learning benefits. However… there’s a limit! There is an optimum level of interactions between them that maximizes learning; going “beyond the optimum” can actually lead to limited or negative returns with respect to their learning benefits (Fowler, 2015). Pretty crazy hey? I guess this is a case of “too much of a good thing”?

Questions Linger

A few questions still linger as I come down from learning all this new stuff. Perhaps you can help? 🙂

If contact with environment can trigger particular genetic “programs”, does this mean that genes also determine student learning capabilities? If that’s the case, is there some way we can engineer environments to “trigger the right programs”, while avoiding the “wrong” programs?
I referenced manipulation of sliders earlier when referencing a VLE. Does this type of interaction actually “count” as physical interaction, or does embodied learning need to incorporate gross motor skills, for example?
How does one determine the optimum level of interaction between the representational fidelity and learner interaction of a VLE?
- I mean, I feel like The Legend of Zelda: Breath of the Wild does a pretty dang great job of mixing these two and teaching the player without using any words, but how did they find that exact sweet spot without leading to negative returns?
Bonus Question: I’ve never participated in a distance/online course that takes full advantage of any of the affordances of TELEs and VLEs. Has anyone else?

Thanks for reading, and apologies for being late here. Kinda struggling to keep my head above water at the moment.

Scott

References

Dalgarno, B. & Lee, M. (2010). What are the learning affordances of 3-D virtual environments? British Journal of Educational Technology, 41, 10-32.

Fowler, C. (2015). Virtual reality and learning: Where is the pedagogy?. British journal of educational technology, 46(2), 412-422.

Winn, W. (2003). Learning in artificial environments: Embodiment, embeddedness and dynamic adaptation. Technology, Instruction, Cognition and Learning, 1(1), 87-114.

Appendix

There were a few extra things I came across that were very interesting but would have made the body of the post even longer than it already was. I still wanted to share them because of how useful they seem. Mainly there’s a Table, a Figure and supporting Context, which all relate to a “design for learning” framework for deriving appropriate learning activities. In essence, these resources can help teachers clearly define the learning context before learning takes place in order to maximize effectiveness.

Specifically, the learning context should include/combine variables such as:

Locus of control (teacher or learner)
Group dynamics (individual or group)
Teacher dynamics (one-to-one, one-to-many, many-to-many)
Activity of task authenticity (realistic or not realistic)
Level of interactivity (high, medium, or low)
Source of information (social, reflection, informational, experiential)

The idea is that combining these variables based on the requirements of a given learning context can help a teacher determine the most appropriate teaching and learning approach.

Finally, the Table 1 and Figure 3 below (Fowler, 2015) are meant to be used to help derive learning activities that will take place within this clearly defined learning context. I hope you find them useful!

(Fowler, 2015)

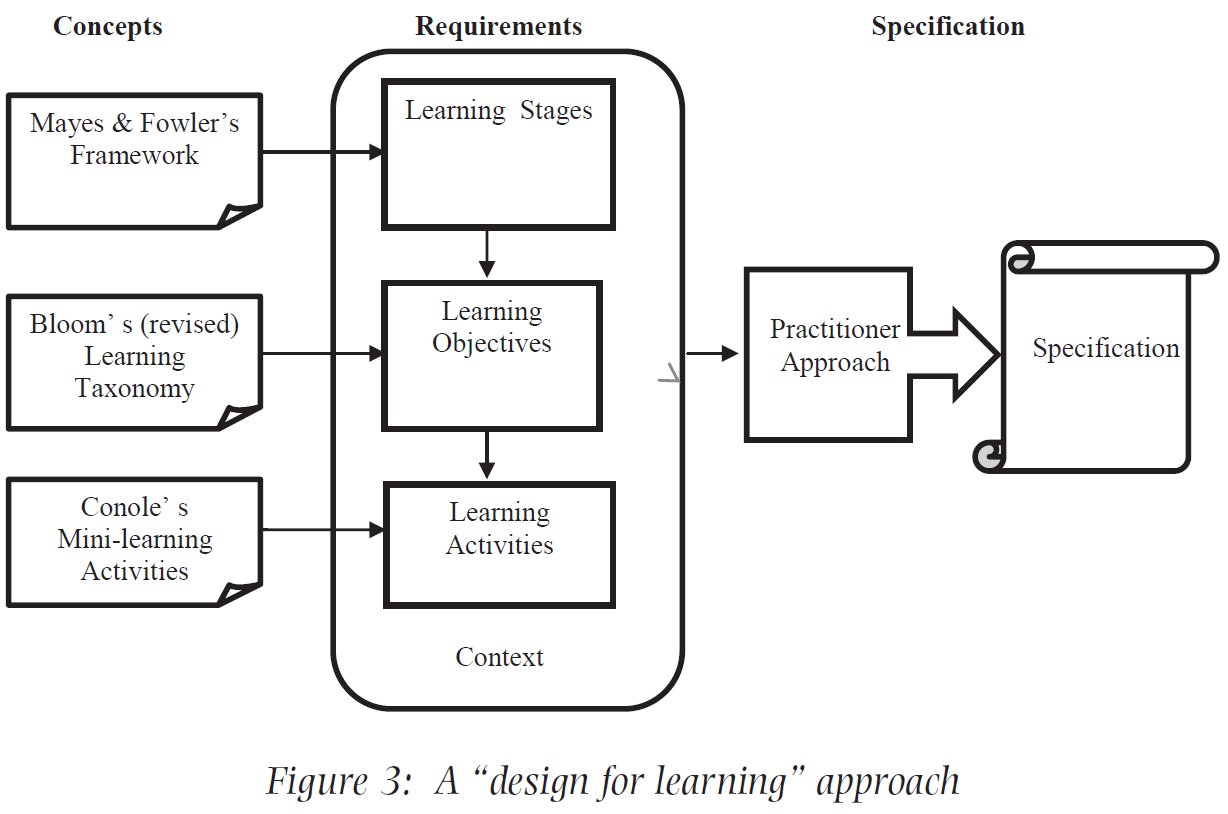
(Fowler, 2015)

Weekly Goals?

Hi, has anyone been able to find the weekly goals referenced in the Overview of Module B? I’ve been marching on ahead without them but… do they exist? And if so, could someone direct me to them?

For those wondering, what I’m referring to is the following statement in Overview: “In the Course Information, Assignments, Assignments 2 option, you will find a suggested sequence of weekly goals (suggested targets) for completing the TELE design option beginning in this module.”

Thanks,

Scott

TELE Takeaways

Apologies for being late on this; it’s been a crazy week! I tried to summarize this Module’s learning in the table below. I took inspiration from a few of you fellow classmates for the structure of the table. I found it very tough to settle on one but I suppose there’s not always a “best” way! Without further ado…

TELE	Key Takeaway	Fundamentals	Strengths	Weaknesses
Anchored Instruction and JASPER	Problem solving using authentic scenarios.	Video-based format Narrative with realistic problems Generative format Complex problems Embedded data design Related, cross-curricular “adventures” Teaches in domains rich in content and application. Cognition and Technology Group at Vanderbilt (1992)	Videos are ideal for conveying learning objectives effectively in a short time span (Eades, 2015). Meaningful content anchored in real-world scenarios helps motivate students. Constructivist nature allows students freedom to make sense of the content in their own way. Model is especially conducive to group work. (Vanderbilt, 1992) Students given chances to correct initial misconceptions. Teacher used as a resource or guide, not authoritative provider of knowledge.	Digital video is the predominant tech, so there’s less chance to engage with the teacher than with fellow students. Lack of direct instruction could be very challenging for some students. Historically speaking, most “educational” videos don’t age well, although it may be better now that almost all common cameras are of good quality.
SKI/WISE	Tackling misconceptions through scaffolding.	Heavily weighted toward scaffolding. Key pieces are instruction, experience, and reflection. Tenets are to 1) make (student) thinking visible, 2) make science accessible, 3) help students learn from each other, and 4) promote lifelong learning. Strong focus on misconceptions. (Linn, Clark, & Slotta, 2003)	Strengths of constructivist approach are amplified by having prior knowledge assessments and an inquiry approach built into the framework. Each lesson follows a standard structure that has been shown to be effective for student learning. Opportunities for collaboration, reflection, and feedback are fundamental to the approach.	Heavy focus on scaffolding and misconceptions may not motivate students if they are not interested in the given subject matter. Teachers may find the structure overly prescriptive and difficult to adapt on-the-fly. Time-consuming for teachers to determine if a topic or subject could fit into the WISE template. Doesn’t really offer many advantages over other constructivist frameworks.
LfU	Motivating students through integration of content and process.	Focus on three stages: 1) Motivation, 2) Knowledge Construction, and 3) Knowledge Refinement. Motivation is the driving force for the model. Highly constructivist in nature. Heavy focus on lesson design and ensuring that learning activities meet the learning objectives. (Edelson, 2001)	Motivation and refinement stages of learning, often sideswiped by attempts to communicate knowledge, take centre stage in this model. Focus on helping students experience the “need for knowledge”. Process knowledge is as important as content knowledge. Students are provided opportunities to see how what they are learning could be used. The framework includes a simple yet extremely detailed table on how to apply LfU.	LfU’s flagship activities are showing their age or are inaccessible, a reminder that building lessons on specific tech could eventually render the lesson obsolete. There remain numerous topics in traditional K-12 schools for which it would be extremely difficult to apply LfU. Teachers must be masters of the topic approached using this method in order to comfortably and effective balance the investigation-discussion cycle. PD on how to use the tech required to design elaborate LfU lessons may be required.
T-GEM	Model-based data-driven approach.	Inquiry-based and iterative approach using a data-driven model. Students compile information then 1) Generate a relationship, 2) Evaluate the relationship, and 3) Modify that relationship. (Khan, 2007)	Students are steeped in learning activities that emphasize critical thinking and reflection. Students are encouraged to think like scientists and gain experience working with real data.	Approach is student-centred but requires an extreme amount of work on the teacher side to ask the appropriate guiding questions to effectively scaffold each student. Teachers must be highly experienced in the subject being taught.

The most obvious threads I perceived to be weaving through each model are, in alphabetical order, collaboration, constructivism, inquiry, motivation, and a focus on connecting activities to “real life” contexts. Well, maybe not so much with T-GEM, as it’s slightly more concerned with relationships between data than real-life contexts, but still. I can honestly say that every single one of the models, if used even partially appropriately, would likely be more beneficial to students than any traditional chalk-and-talk for an appropriate topic. So much time and effort has clearly been poured into ensuring that these models/frameworks/whatever-you-wanna-call-’em take into account the unique students who are there in the classroom to learn. Misconceptions are noted, explored, modified or totally quashed. Scaffolding is an inextricable part of each model’s lesson design. Tech is leveraged in a meaningful way with a strong focus on visuals. And speaking of visuals, I was quite gobsmacked by the amazing tables and visuals you all created for this posts. I hope you don’t mind if I steal them!!

I must say that I really, truly enjoyed this Module. The number of practical takeaways was exceptional, and the LfU model resonated so strongly with me that I still can’t comprehend how I didn’t know about it sooner.

However, in the face of all of these great resources, each with clear benefit to students, we still see it so rarely in the average class. Why is this? Perhaps it’s the teacher’s inexperience with branching out in such a student-centred, constructivist way? Perhaps it’s being too settled into a routine where “the resources are all ready” and it’s a one-size-fits-all model where the teacher feels the lesson has been “perfected” even before they meet the students who will be engaged in the lesson? Perhaps it’s simply the absolutely massive amount of time, skill, effort and cyclical revisions required to make these lessons successful, and ensure each student gets the full benefit of the material? I don’t know the answer. I will certainly be thinking about this going forward, both in my TELE design as well as in my job as a Math department head. Is there anything I can do to convince/motivate my teachers to do things a little differently?

-Scott

(sorry for the weirdly-formatted table I couldn’t figure out how to align it to the top and left-justify it!!)

References

Cognition and Technology Group at Vanderbilt (1992a). The Jasper experiment: An exploration of issues in learning and instructional design. Educational Technology, Research and Development, 40(1), 65-80.

Edelson, D.C. (2001). Learning-for-use: A framework for the design of technology-supported inquiry activities. Journal of Research in Science Teaching,38(3), 355-385.

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Linn, M., Clark, D., & Slotta, J. (2003). Wise design for knowledge integration. Science Education, 87(4), 517-538.

Teach-’em with T-GEM!

One concept that my students find particularly challenging is circuits. Students seem to be OK if I’m simply giving them values such as voltage, resistance, and/or current, and asking them to toss those into Ohm’s law and see what the result is. However, once the questions become more theoretical (“why is there less current flowing through the higher resistance?”, “why does the current flowing through two parallel resistors equal the current before it splits, and after they recombine?”, and so on) the students struggle more and more. Even just mentioning “series and parallel circuits” is often enough for about half my class to shudder with disgust and tell an anecdote about why they hated this topic last time they encountered it.

Clearly there’s an issue there. To name just a few, I feel it’s a mix of 1) teachers not appropriately setting up and explaining the concept, 2) not giving enough analogies to make it “real” to them, 3) focusing too heavily on plug-and-play style questions and 4) electricity being, essentially, an invisible process without the help of visual simulations. I think approaching these electricity concepts using simulations supported by T-GEM could really make a difference, as they can, in the words of Samia Khan (2011, p. 227), “process large amounts of information and view representations in multiple ways”.

T-GEM is a framework or, perhaps more accurately, a cycle, and one I only first encountered in this week’s readings. Like in many other weeks, I was really pleased by how much sense it made while also being frustrated it isn’t implemented more often. I can see it being implemented for teaching circuits, and sketched out an idea for this to be paired with PhET’s HTML5 “Circuit Construction Kit: DC – Virtual Lab” . I chose an HTML5 activity to allow it to be accessed on any mobile device. I started brainstorming ways that the simulation could be used to extend the learning experience past tedious Ohm’s Law calculations. I organised my (still sketch-like) thoughts using a table, inspired by Khan’s table in New Pedagogies on Teaching Science with Computer Simulations (2011, p. 223). Feedback/comments/criticism welcome!

Major phase of (T-)GEM	Main teaching methods	Teacher guidance strategies	Computer simulations
Compile information	Ask students to locate data on a variety of series and parallel circuits (currents, resistances, and voltages across components) – simple circuits can be found online	Demonstrate how to determine which variables/units relate to which measurement	Teacher could recreate simple circuits using the PhET simulation and confirm the variables. Any extra information such as “Show Current” should not yet be shown.
Generate relationship (G)	Identify variables for students (V, I, R)	Direct students to “Labels” feature to help them	Ensure students only explore the first set of components in PhET. Switches, alternate voltages courses, items should be hidden.
	Ask students to find trends	Focus students on simple circuits first, approaching series and parallel circuits separately.	If found circuits are recreated using PhEt, Turning on “Values” could help students find trends
	Ask students about relationships between V, I, and R for series and parallel circuits	Focus students on simple circuits first, suggesting they approach series and parallel circuits separately	Students could be encouraged to keep track of data in a table with separate columns for V, I, and R
		Ask students to make incremental changes	Student could be encouraged to change variables in tiny increments, such as adjusting a single resistor’s value or adding a single battery
		Ask students to compare one circuit to another	More than one instance of the simulation could run at once, on various devices, allowing for cross-classroom comparisons
		Ask students to explain	Teacher could allow “Show current” and have students discuss what changed when adding multiple resistance in series versus in parallel
Evaluate the relationship (E)	Provide discrepant information	Ask students “why isn’t current flowing in this circuit?”	Teacher could use the simulation to create a circuit that seems like it should work but current is not flowing in one or more branches (connections not logical, too much resistance compared to another branch, etc”
		Ask students “why is this circuit on fire?”	Teacher could set up a short circuit and have students explain why this circuit is not safe using appropriate terminology (current, resistances)
	Provide an extreme case	Ask students “does this make sense?”	Teacher could have students set up circuits that have a huge number of components (15+ parallel resistors, 15+ light bulbs in series) and see if their hypotheses about circuit function holds up
		Ask students “why doesn’t this work?”	Teacher could ask students to each create 3 different circuits that don’t work for some reason, and explain why
	Provide a confirmatory case	Ask students to predict	Teacher asks students to make a prediction about a series or parallel circuit (and its values for voltages, currents and resistance) before using the simulation to confirm their prediction
		Do not correct students	Have students work together to create circuits following specific conditions (x number of series pieces, y number of components), fully solving the circuit on paper before creating it together and using the provided Voltmeter and Ammeter to confirm prediction
		Ask students to compare	Task several groups with the same circuit and have them all compare results
Modify the relationship (M)		Ask students to revisit their original relationships between V, I and R	Have students reflect in writing or through discussion on how their original ideas did or did not hold up in the face of each new case
		Ask students to summarize relationships	Have students rewrite what they understand about the relationships between voltages, currents and resistances for series and parallel circuits, having them refer to examples/circuits covered in the activity
		Ask students to solve a new case	Provide students with a very complex case involving series and parallel components and have students completely solve it (find all voltages, currents, and resistances) by working together and leveraging the PhET simulation

Oh, you’re still here! Thanks for reading 🙂

Reference

Khan, S. (2011). New pedagogies on teaching science with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.

LfU and You!

I was shocked that I had not encountered the LfU framework prior to this week. It seems to pull many of the concepts and theories that resonate with me into a nice package, and one that is meant to be easily applied to design activities. Brilliant!

Specifically, I enjoy how it leverages some of the most powerful aspects of constructivist, cognitivist and situated learning perspectives (Edelson, 2001, p. 357) and makes them concrete by providing specific criteria that each activity must meet — motivation, knowledge construction, and knowledge refinement, (I started calling it MCR). The paper even provides an amazing reference table that I promptly recreated, which I’ll append to my post.

If I was in the classroom this term I would want to jump on this framework immediately and try it out. Even so, I can think of a number of ways I might use it. I have been trying to pick apart Desmos from all angles this term, and so in searching for neat activities I stumbled upon Will it Hit The Hoop? (http://bit.ly/2clkfWj)

— For context I recommend you quickly try out the Student Preview, it’s pretty great —

Here are my thoughts about the activity, organized using the Table 1 from Edelson’s paper:

Step	Process	Design Strategy
Motivate	Experience curiosity	The activity starts by having students attempt to fit a basketball shot with a line of best-bit. Noticing this in real-life context, with help from a video, could elicit curiosity and cause students to address the problematic gap or limitation in their understanding of how basketballs travel.
	Experience demand	Students are encouraged to guess answers early in the activity, but later questions create a demand for the knowledge as they require students to have explored previous questions, and use what they have learned about quadratic functions and parabolic motion. The extension activities cannot be solved unless their knowledge is applied.
Construct	Observe	The introductory activity paired with videos of real-life basketball shots provide direct experience with the novel phenomena they are exploring (considering the flight of a ball frame-by-frame), and in order to make the predictions expected of them early in the activity they must be observant.
	Receive communication	Early in the activity, students will be providing a range of answers to the prediction questions followed by small-group and whole-class discussions. This communication on several scales allows students to learn from one another (ZPD comes to mind), as well as start to build new knowledge structures based on the communications taking place.
Refine	Apply	In order to take their new knowledge structures from declarative to procedural form (Edelson, 2001, p. 359) it must be applied. This activity expects students to make use of their new knowledge structures, using the real-life videos and discussions as indices, to analyze basketball shots using mathematical equations. This direct manipulation of graphs, when overlayed on top of an image/video of a contextually-relevant basketball shot, reinforces what they have learned. Follow-up questions, analysis of actual student predictions with and without mathematical help, and extension questions, meshed with ongoing discussion and teacher guidance, all help students to reorganize their understanding into a useful form.
	Reflect	Opportunities for reflection are woven into the activity at key points to force students to reflect on what they have observed or learned up to that point. This allows them to reorganize and reindex their knowledge prior to having to extend their new knowledge structure when information is encountered later in the lesson. Note: The manner in which these reflection questions were incorporated reminded me of the structure of My World GIS, where investigations and discussions were spread out to allow incremental mastery of a concept. This is an excellent strategy that ensures that students are able to transfer information from short-term memory to long-term memory by rehearsal *before* they encounter new information.

If I were delivering this lesson I would likely incorporate an over-arching reflection session at the end which forces students to process everything they had learned. I would then, depending on the skill level (and Grade level) of students, love to have them do their own experiment where they take their own videos of throwing a ball and confirm that even their own throws can be modeled using mathematics. This would encourage even further buy-in for the students than a video of someone else.

What does LfU afford students and teachers?

Well, it should be clear by its very name, learning-for-use. Well-designed activities would finally remove the need for students to ask “when will we ever use this?” because the activities are steeped in real-world contexts.They should, due to their constructivist/cognitivist nature, be designed to set students up for success because they are highly student-centred. Having to consider motivation, construction, and refinement of knowledge before even delivering the activity ensures the students will walk away having been afforded far more than a one-way lecture ever could have. For teachers, LfU provides clear direction both in the design and facilitation of each activity, and allows ample opportunity for teachers to guide and facilitate. It’s a win-win.

But what if students still ask, as they often do, something like “when will we ever use this in real life? I mean, it’s not like calculating trajectories and creating parabolas will help us on a basketball court”. Which is true, they probably won’t. But, the concepts they learn, the understanding and knowledge of the processes they will have internalized, could help them to extend what they learn and apply them to future projects. The teacher could discuss with them the power of these equations – how they are one way to truly predict the future. I bet they couldn’t do that before. The main point is that once they understand that all objects launched adhere to these rules (barring air friction) then the world is their oyster; they could use the concepts to create their own catapult even, or use the equations to program their own computer games. Actual, honest-to-goodness real-life skills. Neat!

References

Bodzin, A. M., Anastasio, D., & Kulo, V. (2014). Designing Google Earth activities for learning Earth and environmental science. In Teaching science and investigating environmental issues with geospatial technology (pp. 213-232). Springer Netherlands.

Edelson, D.C. (2001). Learning-for-use: A framework for the design of technology-supported inquiry activities. Journal of Research in Science Teaching,38(3), 355-385.

My World GIS videos, ETEC533 Module B.

Appendix – Table 1 from Edelson (2001)

Step	Process	Design Strategy
Motivate	Experience demand	Activities *create a demand* for knowledge when they require that learners *apply* that knowledge to complete them successfully.
	Experience curiosity	Activities can *elicit curiosity* by revealing a problematic gap or limitation in a learner’s understanding.
Construct	Observe	Activities that provide learners with *direct experience* of novel phenomena can enable them to *observe* relationships that they encode in new knowledge structures.
	Receive communication	Activities in which learners receive direct or indirect *communication* from others allow them to *build* new knowledge structures based on that communication.
Refine	Apply	Activities that enable learners to *apply* their knowledge in meaningful ways help to *reinforce* and *reorganize* understanding so that it is useful.
	Reflect	Activities that provide opportunities for learners to *reflect* upon their knowledge and experiences retrospectively provide the opportunity to *reorganize and reindex* their knowledge.

Jasper’s Anchored Adventures

How does this technology support learning and conversely how might it confound learning? What suggestions do you have for how the Jasper materials or other digital video might be utilized in your context (include suggestions for activities that do not involve the videos)? What research supports your suggestions? How might the video and/or the activities be augmented for children with learning issues in math? How have or can the contemporary digital technologies and/or their websites also support these suggestions for children with learning issues (eg. Prodigy, Desmos, King of Math, Math Bingo, Reflex Math, or others).

From what I can tell after reading and learning about Jasper, I see it much less as a “technology” than I see it as an approach to instructional design. In their Jasper project, the Cognition and Technology Group (1992) used a set of design principles (see Figure 1 below) to create videos and lessons using an “anchored instruction” approach. The intent of these lessons and their video-based format was to expose students to complex, real-world problems that challenge them to come up to solutions to problems that are not clear-cut. Jasper designed these videos and lessons to emphasize the importance of “generative activities on the part of students” (Cognition and Technology Group at Vanderbilt, 1992, p. 76), with the intention of allowing students to work in cooperative groups that allow space for them to self-correct without much teacher intervention. This idea of students generating their own solutions, constructing their own knowledge, as well as building off each other skills and strengths, related strong constructivist fundamentals, reminding me of our old pals Piaget and Vygotsky.

Figure 1

This “anchored” approach, supported by videos, allows students give context to the curriculum, meaningfully connecting it with their lives in a way that would otherwise have been impossible through textbook problems. By introducing a variety of problems in the context of a story, or “adventure”, students may be more motivated to work together on potential solutions to questions that more than a single answer. Finally, by moving from Direct Instruction (Model 1) and structured problem solving (Model 2) toward guided generation (Model 3), students have a genuine opportunity to develop their problem-solving and critical thinking skills. However, the success of this design in practice, of course, still depends to some extent on how well it is introduced and facilitated.

Model 1: Basics First, Immediate Feedback, Direct Instruction

Model 2: Structured Problem-Solving

Model 3: The “Guided Generation” Model (applies concept of constructivist scaffolding)

-Cognition and Technology Group, 1992

Speaking of success, the question above asked how the technology may confound learning. I had a few thoughts on this:

The lack of direct instruction may be extremely off-putting, or even frustrating, for students with little experience with open-ended or inquiry-based learning scenarios.
Videos “[are] used as the instructional medium because of [their] engaging characteristics” (Hasselbring, 2005), and are ideal for conveying lots of information in a short time-span, but this could be confounding to some students. The Jasper videos were short and concise, but the scenarios were described quickly and the problems flew by. Students who take longer to process information or who like to write notes may find this frustrating or stressful, especially if they are not able to rewind the video. Thankfully 2018 and YouTube lessens this problem. I’m not so sure about 1989 LaserDiscs. Although videos are an ideal platform for showing students visuals that connect concepts with everyday experiences, and videos
Just because students are shown a video doesn’t mean they will be engaged by/with it. To refer back to the Jasper project, students who don’t have any interest in ultralights and mechanics may not find interest in calculating fuel consumption and airspeed velocity, even when the problems are presented in a more entertaining way than paper or direct instruction.

To refer to my own teaching, I would not use Jasper materials in 2018. This is not because they’re poorly designed, because their design seems sound, but because they’re outdated and cringeworthy.

Do we really need this guy to act out “too much risk”? Probably not… a little too “80s-90s humour” for me… although I make an exception for Bill Nye The Science Guy…

However, I would (and have) used similar resources like Twig to kick-start my lessons. I used to play them a video and have them discuss the concepts, or extend the problem by coming up with new questions based on what they learned from it. When teaching Physics I’ve often used PhET to amplify lessons with interactive content, and have designed a number of student-paced and student-centred activities which have student use PhET’s HTML5 applets to explore tricky introductory concepts like planetary orbit, Newton’s Laws, momentum and even time dilation. I also have begun using Desmos more and more in classes to relay complicated concepts (Fourier Transforms, yeesh!!). By engaging students with more complex, “fuzzy” problems in real-world contexts, supported by these technologies, I hope to steer students away from relying solely on procedural knowledge to solve problems (Hasselbring, 2005).

Jasper’s anchored design has inspired me to consider how else I could apply its approach to future lessons. I particularly like the idea of “embedded data design” and “pairs of related adventures” and plan to steal those in the not-so-distant future.

As for a way that contemporary digital technologies can support children with learning issues, I’d most immediately direct them, once again, to Desmos… yes, please apologize for my current fanboy nature about this tool, but it’s an amazing tool!!! I mean, just check out their activities… Desmos allow students with learning issues to become much more intimately acquainted with the “what”, “how” and “why” of mathematical concepts through scaffolding, collaboration and inquiry-based activities; all this while pushing to increase accessibility for learners with disabilities. There are font-size settings for low-vision users, high-contrast colors, and a specialized graph reader for fully blind students. This, I can pretty much guarantee, was not an option back when Jasper started. I would love for more teachers to jump on board and give it a shot.

In closing, I’ll say that the term “anchored instruction” is one I’ve been looking for for a long time to express my thoughts on how we should approach lesson design, and it’s one I can see myself using more in the future.

Thanks for reading!

Scott

References

Cognition and Technology Group at Vanderbilt. (1992). The Jasper Experiment: An Exploration of Issues in Learning and Instructional Design. Educational Technology Research and Development, 40(1), 65-80. Retrieved from http://www.jstor.org/stable/30219998/.

Hasselbring, T. S., Lott, A. C., & Zydney, J. M. (2005). Technology-supported math instruction for students with disabilities: Two decades of research and development. Retrieved from http://www.ldonline.org/article/6291/.

Morally Scientific

The Great Divide

The Right Stuff

Knowledge Construction

A GLOBE-al Network

Clear Direction… to a Fault?

Cognitive Learning Theory Renaissance

Environment guides Learning

A Variety of Applications

Affordances of VLEs

VLE’s Unique Characteristics

Unique Characteristics of 3D VLEs

Representational Fidelity

Learner Interaction

Questions Linger

References

Appendix

TELE

Key Takeaway

Fundamentals

Strengths

Weaknesses

What does LfU afford students and teachers?