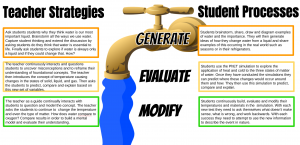
- How can learning be distributed and accelerated with access to digital resources and specialized tools and what are several implications of learning of math and science just in time and on demand?
When I attended high school in the late nineties, I understood math and science to be a list of facts and processes that needed to be learned and later restated on a test from rote memory. I vividly remember my teacher going through an example of completing the square in math class and worrying how I would ever remember every single step. I eventually memorized each step in the correct sequence and ended up doing quite well on the final exam as I recall. But I never really had a strong understanding of the purpose behind this or many other skills or facts I had learned in my many senior classes. I found many lessons lacked relevance and required that I trusted that what I was learning would serve me in the future.
Throughout my 9 year career as a math and physics teacher, I have noticed an evolution in how learning occurs with greater access to digital resources and specialized tools in the classroom. While graphing calculators have remained fairly unchanged in the last 20 years, other digital resources have revolutionized how student acquire, communicate and visualize mathematical and scientific knowledge.
One significant change that I have noticed in last 20 years is that students rely less heavily on their teacher as a source of all knowledge. The fact that a student can revisit posted lessons on the Google Classroom and view an endless number of video lessons on Youtube has empowered students to take full responsibility of their learning. In turn, teachers can spend class time digging deeper into questions without having to worry that they cover every type of question a student may face in their homework. Students also have access to endless information on their devices. Teachers no longer need to teach every trivial fact and can expect students to research things that they need to know. In turn, the teacher’s role has shifted from disseminating knowledge to helping students connect knowledge in meaningful ways. Teachers model how inquiry can lead to startling conclusions and how questions ground learning. I found myself in a chat with some students a couple months back about the economic model of Amazon Prime and whether a Prime membership is worth the annual fee? I decided to postpone my lesson that day and have students investigate when one should purchase a Prime membership and what is the true cost of free shipping. As a result, students were using their numeracy and research skills to formulate arguments and communicate their thinking using substantiating factual evidence. If anything, greater access to digital technologies have reintroduced spontaneity and creativity back into the math and science classroom and improved student engagement in authentic problem based learning.
Greater access to digital resources has also revolutionized how students visualize and experience scientific phenomena. When I took Biology 12, I can recall learning from many diagrams in textbooks, such as this one, describing processes such as DNA replication. I can remember spending endless hours creating and refining my mental model of each process without truly knowing whether my model was entirely correct. Today, students have access to endless visualizations and simulations that provide an empirical understanding of many processes. This video, for instance, showcases DNA replication in far greater acuity than any diagram ever could. This simulation, as another example, affords students not only the ability to observe the unobservable but to explore various variables pertaining to the process. In effect, digital resources allow students to visualize, explore, to predict and play with natural phenomena like never before. In turn, students are better able to construct knowledge in meaningful ways all the while satisfying their need to inquire about the natural world around them.
This misconception could be associated with students transitioning from operations with whole numbers to operations with fractions because, to them, the rules have changed. Because of previous “knowledge”, the students performed operations distinctly, considering the numerators and the denominators in separate operation. In order to teach additions and subtraction involving fractions, it is important to impress upon the students that the numerator indicates the number of parts and the denominator indicates the types of part (the whole). The computational rule usually don’t help students think about the operations and what they mean. When the students are only armed with rules, even when the rules are mastered, it is quickly lost in the short term as the myriad of rules soon become meaningless when mixed together (On complex operations).
This example will shake the misconception. The students will be encouraged to connect the meaning of fraction computation with whole number computation such as ¼ is one part out of four equal parts of a whole. In order to practise addition of fractions with same and different denominators, the students will use the interactive activity 
The aim of this model is to help the students learn to think about fraction and the operation, to contribute to mental methods, and provide a useful background when they eventually learn the standard algorithms of LCM.
