Antiderivative

If we know the derivative of a function, the process that we try to find its origin function is the antiderivative.

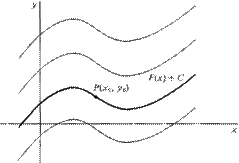
However, the derivative of a constant is 0, we can not determine which constant is in the origin function, so we can just find a set of functions which all have a derivative like this.

For instance, if f(t)=t is the derivative of F(x)

We need to figure out which function has a derivative equal to t.

By doing the opposite operation of differentiation, it is easy to find out one of the origin function F(t)= ½ t^2

As we know, the derivative of a constant is 0, so we can not determine what the certain original function is. In fact, all the function F (t)=½ t^2 +C (C can be any number) have a derivative equal to f(t)

Integration

Integration can be classified into definite integration and indefinite integration. Indefinite integration exactly has the same meaning of antiderivative. The indefinite integration of a function f, which is also known as the antiderivative of a function f, is a function F such that F′=f, while the definite integral is just a number. The definite integration of a function is equal to the area under the function on a certain domain.

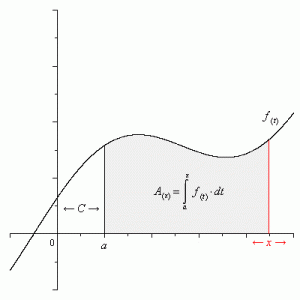
As the picture shows above, the grey part is the indefinite integral of the function f (t).

If we replace variate twith a certain number, it becomes the definite integration of the function f (t).