If we want to find the area of the UBC fountain without using π, how can we do just with the radius r?

We can regard this fountain as a circle.

The question is, without π, just with radius r, how can we get the area of a circle?

First, we divide this circle into eight parts and calculate the area of these four triangles. Then, we can roughly get the area of the circle.

Then, I divide this circle into sixteen parts, only regard the area of these eight triangle as the area of circle, we can find the “extra” area is smaller than last graph.

Then, we make a hypothesis that, if we can divide this circle into 2n parts, regard the area of the triangle as the area of circle, the “extra” area will become smaller and smaller, and our result will be more precise.

The process like this is also like the process of integration.

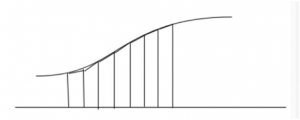
But the difference is, if we want to integrate a function, we need to cut the area ,which is between x axis and the curve, into many pieces and calculate the area of each pieces and add them together. If the number of pieces is big enough, we will get more precise number of the area between x axis and the curve.