Skip navigation
- Showing students steps (specifically labeling step 1, 2, 3, etc.) may help, but we also need to consider whether this will create a frame that limits students’ creativity, critical thinking, and analyzing ability, as they may just memorize the steps and mindlessly apply them to similar questions without thinking. The original purposes for us to show steps when teaching are 1) to demonstrate systematic approaches toward solving problems, and 2) to organize the explanation so that the whole concept behind can be clarified and simplified. Therefore, I would show steps and also inform students that they are not required to follow the exact steps, on the exam they will not be judged on whether they are following the same steps as in class, the proper justification is the one we are looking for. If they have some other steps/approaches to find the correct answer they are free to do so, and if they are not sure whether their steps/approaches are correct or not I would be happy to discuss with them. This links to autonomy that we have talked about in general.
- Fun diagrams for illustration.
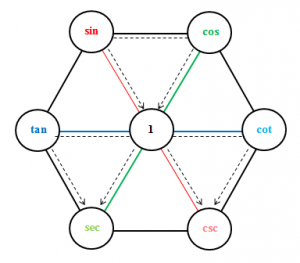
- Mnemonic diagrams for students to visualize the concept. For example the diagram below can be very useful for students to visualize the relationship among trigonometric ratios and therefore turn the concept into their long term memory:
- Story telling can be an effective way to engage students’ interest in the very beginning of unit.
- Sometimes linking dry math concepts to teen culture content can give students a bit of brain break and involve them into the world of mathematics that terrifies many people. For example:
- When I went over the integer sign (a bold Z), I refer to that sign as a “Dragon Ball Z” sign to entertain my IB students.
- When I went over the end of solution/proof sign (tilted # sign), I refer to the sign as a “Instagram Hashtag” sign.
