January | 2017

Definition

Antidifferentiation:

If f(x) is a function, then an antiderivative of f(x) is another function F(x), such that F'(x)=f(x).

Intergral:

If f(x) is a function, then the integral of f(x) over the interval [a,b] is the limit of its Riemann Sum over that interval (if it converges).

Difference

For anti differentiation , if there is an anti derivative, there are infinite function F(x): F(x)+1, F(x)+1/2, F(x)+pi, they can be concluded by F(x)+r,r is any real number. There is no special antiderivative for a function, they’re all on equal footing.

However, integral gives the area under the function f(x) between x=a and x=b.

This means that the integral of a function is a number that is special.

Take an example, we have a function f(x)=3x^2.

The anti derivative can be F(x)=x^3+1,or F(x)=x^3+3…

However,the integral from 1 to 2 is \int_1^2 3x^2 dx=8, which is special.

So we know that anti derivative is not special for a function but integral is special for a function.

Denises Wang 24482168

Yuki Zhang 50653161

That is what I have now. A function f(t) and quadrant on my paper. If I want to calculate the area under the function, motivation of integration appears.

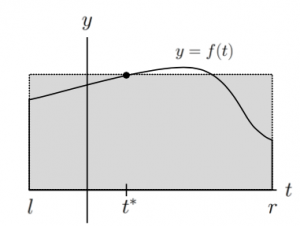
We set two different number on the x-axis like l and r, making it a interval [l,r].Then we find a number in this interval,t,and calculate the value of f(t).

So the area approximately equals to f(t*)·(r-l)

For the deeper and more precise calculation, we divide the interval [r-l] into three equal sub-intervals like t1, t2 and t3.

Then t1=t2=t3=(r-l)/3.

And we find three number t1*, t2* and t3* which within three sub-intervals respectively, calculating their value of y-axis such as f(t1*), f(t2*) and f(t3*)

Therefore, the refined area under the function can be presented as A=f(t1*)·t1+f(t2*)·t2+f(t3*)·t3

With this trial, we can divide [l,r] into more and more sub-intervals to reach the most precise area that I want to calculate.

Of course, area only can be calculated in some functions like continuous functions, for the reason that a non-continuous function does not have closed area.

Written by Yuki Zhang(50653161) and Denise Wang(24482168)

wings

Just another UBC Blogs site

Monthly Archives: January 2017

The difference between integration and antidifferentiation

Definition

Antidifferentiation:

If f(x) is a function, then an antiderivative of f(x) is another function F(x), such that F'(x)=f(x).

Intergral:

If f(x) is a function, then the integral of f(x) over the interval [a,b] is the limit of its Riemann Sum over that interval (if it converges).

Difference

For anti differentiation , if there is an anti derivative, there are infinite function F(x): F(x)+1, F(x)+1/2, F(x)+pi, they can be concluded by F(x)+r,r is any real number. There is no special antiderivative for a function, they’re all on equal footing.

However, integral gives the area under the function f(x) between x=a and x=b.

This means that the integral of a function is a number that is special.

Take an example, we have a function f(x)=3x^2.

The anti derivative can be F(x)=x^3+1,or F(x)=x^3+3…

However,the integral from 1 to 2 is \int_1^2 3x^2 dx=8, which is special.

So we know that anti derivative is not special for a function but integral is special for a function.

Denises Wang 24482168

Yuki Zhang 50653161

Motivation of Integration

That is what I have now. A function f(t) and quadrant on my paper. If I want to calculate the area under the function, motivation of integration appears.

We set two different number on the x-axis like l and r, making it a interval [l,r].Then we find a number in this interval,t,and calculate the value of f(t).

So the area approximately equals to f(t*)·(r-l)

Definition

Antidifferentiation:

If f(x) is a function, then an antiderivative of f(x) is another function F(x), such that F'(x)=f(x).

Intergral:

If f(x) is a function, then the integral of f(x) over the interval [a,b] is the limit of its Riemann Sum over that interval (if it converges).

Difference

For anti differentiation , if there is an anti derivative, there are infinite function F(x): F(x)+1, F(x)+1/2, F(x)+pi, they can be concluded by F(x)+r,r is any real number. There is no special antiderivative for a function, they’re all on equal footing.

However, integral gives the area under the function f(x) between x=a and x=b.

This means that the integral of a function is a number that is special.

Take an example, we have a function f(x)=3x^2.

The anti derivative can be F(x)=x^3+1,or F(x)=x^3+3…

However,the integral from 1 to 2 is \int_1^2 3x^2 dx=8, which is special.

So we know that anti derivative is not special for a function but integral is special for a function.

Denises Wang 24482168

Yuki Zhang 50653161

That is what I have now. A function f(t) and quadrant on my paper. If I want to calculate the area under the function, motivation of integration appears.

We set two different number on the x-axis like l and r, making it a interval [l,r].Then we find a number in this interval,t*,and calculate the value of f(t*).

So the area approximately equals to f(t*)·(r-l)

We set two different number on the x-axis like l and r, making it a interval [l,r].Then we find a number in this interval,t,and calculate the value of f(t).