Homework #1 Download here. Solutions here, or below. With a PDF Plugin, the exercises should load here. With a PDF Plugin, the solutions should load here.
question from a student: About the last example of the first lecture. After converting cos(2kx) into its exponential form, when we are trying to combine the two fractions, how do we know what to do? I mean, to do v = -n and then v = -m ? Reply ↓
We’re looking at: The idea is to collect like terms. Notice, for example that shows up twice, once for and again when . Reply ↓
when doing question 3, will the summation change when I assume v=-n? In the class note it seems the summation will not change. Reply ↓
If you make a substitution, like v=-n, the formula for the sum can look different but it will still add up to the same thing. Reply ↓
I assume you mean , as in the top of page 4 of the solutions. It does not show up because the general solution looks like: and . Reply ↓
question from a student:
We’re looking at:
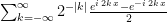
The idea is to collect like terms. Notice, for example that shows up twice, once for
shows up twice, once for  and again when
and again when  .
.
when doing question 3, will the summation change when I assume v=-n?
In the class note it seems the summation will not change.
If you make a substitution, like v=-n, the formula for the sum can look different but it will still add up to the same thing.
Question Posting is not working for HW#2 and HW#3.
Fixed. Sorry about that.
for the solution of #6, how come L=6 is not shown in the general solution?
I assume you mean , as in the top of page 4 of the solutions.
, as in the top of page 4 of the solutions.
It does not show up because the general solution looks like:
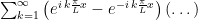
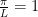 .
.
and