For question 2 a where you use partial fraction to go from (Z/Z-i)(Z/Z+1+i), would you be able to clarify how you found those coefficients A and B? Is there a good way to do partial fractions when you have complex numbers in the denominator? I apologize if this seems simple, I may be missing something basic but I cant get the same answer.
To get the coefficients,
and compare the numerators, as usual. You should get: and
Another way to write the answer is and
( to get the numbers in the answers sheet, multiply by )
Is a mistake in question 5b? The roots that have been found might not be correct. Could you please check that and confirm?! The roots I found are and .
For 2 b is there a short way to find a, b, and c in the PFE? Multiplying out all the terms is really a big mess, and the residue method doesn’t seem to work because of the ‘z’s in the numerator. Thanks.
For question 2 a where you use partial fraction to go from (Z/Z-i)(Z/Z+1+i), would you be able to clarify how you found those coefficients A and B? Is there a good way to do partial fractions when you have complex numbers in the denominator? I apologize if this seems simple, I may be missing something basic but I cant get the same answer.
To get the coefficients,

 and
and 
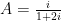 and
and 
 )
)
and compare the numerators, as usual. You should get:
Another way to write the answer is
( to get the numbers in the answers sheet, multiply by
For question 1a, I find 2>|z|>1/5. I understand that it’s an annulus, but I can’t see why -2 and -1/5 are not included for pole. Can you explain?
A pole is where the formula asks you to divide by zero.
-2 is not a pole, because
Question from a student:
Answer:
Guessing isn’t too bad for 2a, but there’s a more systematic way if you prefer:
One method to factor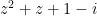 is to substitute
is to substitute 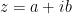 , and then solve for real part and imaginary part equal zero. That is:
, and then solve for real part and imaginary part equal zero. That is:
 and
and 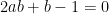
To solve these two equations is then tricky.
Rewrite the second equation as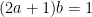 , which inspires us to rewrite the first equation using the pattern
, which inspires us to rewrite the first equation using the pattern  :
:
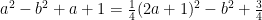
We can then subsitute together and get:
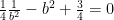
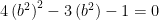
This is a quadratic equation with solutions:

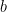 is real, it must be
is real, it must be  .
.
Since
To finish, plug in and find the values of
and find the values of  .
.
What to do after I find the value of a and b?
If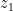 and
and 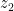 are solutions of a quadratic polynomial
are solutions of a quadratic polynomial  , then that means:
, then that means:
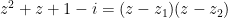
Is a mistake in question 5b? The roots that have been found might not be correct. Could you please check that and confirm?! The roots I found are and
and 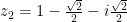 .
.
Yes, a square root was missing. I’ve updated the solutions. Thank you!
Is the answer to 5a missing a ‘z’ in the numerator? What happened to the ‘z’ that was being multiplied by x(z)?
Haha. Yes. Another fix. Thanks!
For 2 b is there a short way to find a, b, and c in the PFE? Multiplying out all the terms is really a big mess, and the residue method doesn’t seem to work because of the ‘z’s in the numerator. Thanks.
I don’t know of any shortcuts for this one.
For Q5b
The roots for (z^2 – 2 Z +1 – i) could be (1 +/- sqrt(i)) as well, right?
because (z – 1 – sqrt(i)) * (z – 1 + sqrt(i)) = (z^2 – 2 Z +1 – i)
No, the roots are unique.
(z – 1 – sqrt(i)) * (z – 1 + sqrt(i)) = (z^2 -2 z +2)