I take it you’re ending up with something like:
The sum is shorthand for :
plug in k=1, calculate the integral, multiply by
plug in k=2, calculate the integral, multiply by
plug in k=3, …
(and add up all the results)
unless k=m, the integral is just going to give zero, so you the sum reduces to:
I am having trouble with matching and solving alpha_k. As in I am left with the integral of u(x,0) * conjugate complex exponentials = alpha_m * 2 * L. Do we manually solve these integrals? I am not able to match what is done in class as a solution.
In question 1a after I convert the sin + sin functions into exponential using Euler’s method, how do I proceed from there? I have looked at the slide mentioned but it only shows that if exponential with power of K’s multiplied by its conjugate(with power of M’s instead of K’s) is either 0 if K does not equal M and 2L if it is.
Try going the other way around, and convert slide 7 into sine functions.
You should get:
For Question 4c, what exactly they mean by the general solution for part b?
The solution to the PDE with inhomogeneous constraints involves and , and the latter requires to have f(x) from the data for the PDE, i.e. u(x,0) = f(x). How can we find the general solution if we are not given f(x)? Or does the question ask about some other solution?
For question 2 when you get to the point of integrating the side with the sum and alpha_k how do we know whether k = m or not?
I take it you’re ending up with something like:



The sum is shorthand for :
plug in k=1, calculate the integral, multiply by
plug in k=2, calculate the integral, multiply by
plug in k=3, …
(and add up all the results)
unless k=m, the integral is just going to give zero, so you the sum reduces to:

Does that answer your question?
I am having trouble with matching and solving alpha_k. As in I am left with the integral of u(x,0) * conjugate complex exponentials = alpha_m * 2 * L. Do we manually solve these integrals? I am not able to match what is done in class as a solution.
You’re on the right track. Usually you only need to solve the integral twice, once for , and again for
, and again for 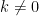 .
.
Question from a student:
This is a separation of variables question, so you’ve made the guess . Plug this guess into the constraints.
. Plug this guess into the constraints.
For example, .
.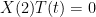 . You don’t want
. You don’t want  , because that makes
, because that makes 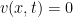 , which
, which is a solution, but not a helpful one. It must be then that  .
.
You plug in
Do a similar thing for , then start solving the ODE for
, then start solving the ODE for  .
.
Question from a student:
Try going the other way around, and convert slide 7 into sine functions.

You should get:
for part 1 , Should this be L/2 instead? If I use 2/L I couldn’t get the correct answer.
Yes, it should. Fixed.
For Question 4c, what exactly they mean by the general solution for part b? and
and  , and the latter requires to have f(x) from the data for the PDE, i.e. u(x,0) = f(x). How can we find the general solution if we are not given f(x)? Or does the question ask about some other solution?
, and the latter requires to have f(x) from the data for the PDE, i.e. u(x,0) = f(x). How can we find the general solution if we are not given f(x)? Or does the question ask about some other solution?
The solution to the PDE with inhomogeneous constraints involves
You’re on the right track. Without , you can still give a formula for
, you can still give a formula for  that includes unknown constants.
that includes unknown constants.
For the solution to 4b):
We had a constraint that Up(2) = -3, but it seems if Up(x) = x +1, then Up(2) = 2 + 1 = 3 (not -3).
Which is right? Just a little confused.
Thank you.
Ah, I missed the minus sign. Fixed. Thank you!