for question two when I split the integral into three parts and end up with only the integral from to of I’m drawing a blank on how to get rid of the absolute value.
Absolute value is a piecewise function, and you can always get rid of it the same way. |\omega| = \left\{\begin{aligned} \omega &&&\text{ if } \omega\geq 0\\ -\omega &&&\text{ if } \omega < 0\end{aligned}\right.[/latex]
(Split the integral again.)
I am having trouble with determining the domain of this function in question 2. It says it is |\omega| < 4\pi[/latex]. How can I determine the domain from this?
When you are taking the Fourier transform, the domain is always the entire real line, here -\infty<\omega<\infty[/latex].
This is different from Fourier series. Note that the transform does not involve a period [latex]{\mathtt T}[/latex].
for question 4. writing q(x) in terms of f(x), the signal from question 1, and rect(x), are you implying to take the derivative of q(x) to get the square wave and then use the differentiation identity as a short-cut?
for question two when I split the integral into three parts and end up with only the integral from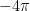 to
to  of
of 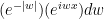 I’m drawing a blank on how to get rid of the absolute value.
I’m drawing a blank on how to get rid of the absolute value.
Thanks
Absolute value is a piecewise function, and you can always get rid of it the same way.
 |\omega| = \left\{\begin{aligned} \omega &&&\text{ if } \omega\geq 0\\ -\omega &&&\text{ if } \omega < 0\end{aligned}\right.[/latex]
(Split the integral again.)
|\omega| = \left\{\begin{aligned} \omega &&&\text{ if } \omega\geq 0\\ -\omega &&&\text{ if } \omega < 0\end{aligned}\right.[/latex]
(Split the integral again.)
Question from a student:
When you are taking the Fourier transform, the domain is always the entire real line, here -\infty<\omega<\infty[/latex].
This is different from Fourier series. Note that the transform does not involve a period [latex]{\mathtt T}[/latex].
-\infty<\omega<\infty[/latex].
This is different from Fourier series. Note that the transform does not involve a period [latex]{\mathtt T}[/latex].
for question 4. writing q(x) in terms of f(x), the signal from question 1, and rect(x), are you implying to take the derivative of q(x) to get the square wave and then use the differentiation identity as a short-cut?
No, you should be able to do it with scaling, shifting and addition.
We’ll talk about the differentiation identity on Wednesday.
OK. Could you please provide me some hint in writing q(x), the slope function, in terms of the rect(x), the square function?
That’s not what the question says – you’re going to need two copies of f(x) too.