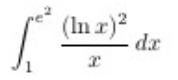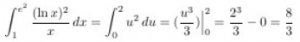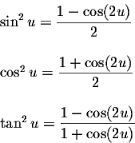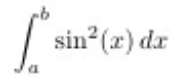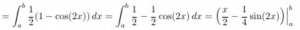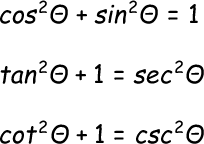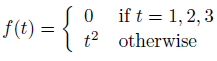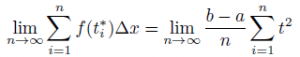Math 100

First Order Differential Equations

Differential equation is a type of equations that contain both a function f and its derivative. First order means that the highest order of differentiation is one. For example, second derivative should not appear in the equation. First order differential equations usually have the form of: dy/dx = f(y, x) .

As we learn in high school, the solution of a funtion is constants. That means we can get an actual number or point by solving the funtion or function group. However, the solutions of differential equations are funtions. In other word, there are more thatn one solution to one differential equation.

One way to solve the differential equations is to represent dy/dx on the Cartisian plane with x and y axis. As we know, the first derivative of a function is its slope. So we are drawing the slope of the solution at every point on the plane. Based on these tangent lines, we can draw a bunch of curves that pass a group of points with corresponding slopes. This is called slope fields, which guide to draw a solution.

An example of slope field: 

Picture comes from: https://www.math.rutgers.edu/~greenfie/mill_courses/math152/diary2.html

Definition of analytic function – A function is analytic at c means that the Taylor series of the function converges to itself at point c. 

In other words, at a point c, there exists a series that exactly equals to the function. For example, e^x is analytic for all x. Because the higher estimated value of e^x, Taylor series, has no difference with e^x.

Infinitely differentiable functions can be differentiate uncountable times and never ended. However, an infinitely differentiate function may not be analytic for all x.  For example the function f(x)=e^(-1/x^2) for all x except for 0, while equal to 0 at x=0. This function is infinitely differentiable but not analytic for x=0.

As for this midterm, the relatively difficult question for me was number 3. This question was not hard, but I was confused by the function inside the integral. Although I knew the fundamental theorem of calculus was the key to solve this, I did not substitute root t before using the theorem. I thought in the wrong way at the beginning and hardly came back. The formula of FTC would help if I were writing down.

Tips to remember:

1. Do not overthink.

Start a question from what you could do. Sometimes rearrange the equation would make it clear. To avoid overthinking, come back to the problem later and try another method.

2. Think of the method or theorem behind the question.

Before answering the question, identify what theorem can be used. Write down the formula of the theorem besides the equation, and then compare.

Before solving an integral, think of all rules that may be helpful based on its characteristics. For instance, to get rid of square root, use u-substitution and square u.  

3. Do not skip steps.

The goal of using substitutions is to simplify the integral. A good substituion can solve it faster. Generally, we want to reduce the power or simplify into a ploynomial. Here are some tips on how to make a substitution in many cases.

1)

In general, we want to arrange the integral into the product of some function f(x) and its derivative f’(x). Then, f(x) would be the u-substitution.

For example:  

Let u = ln x ,  then  du = x^(-1) dx

2)

When we see trigonometric function with a power greater than 1 in the integral, such as sin(x)^2, we want to reduece the power by using the double-angle identities.

For example: 

3)

Trigonometric substitution is useful when we have square root of x^2 plus or minus a constant. For example:   √(x²-1) ,  √(4-x²) …

In this case, we can use the trigonometric identities to get rid of the square root. Some commonly used identities are: 

For example: 

If we let  x = 2sin(t) ,  then  the square root does not involve.

Functions with finitely many removable discontinuities are integrable.

Let f(x) be a defined function on [a, b]. This function has N removable discontinuity, where N is a finite positive integer. We partition [a, b] into n subintervals of width (b-a)/n.

First, we can select all xi* to be non-discontinuous points. Second, we may select all xi* to be the discontinuous points. The area under the curve on the interval [a, b] is the same for above 2 cases.

When n is sufficiently large, the finite number N does not influence the area under the curve. Because N is too small comparing to the infinity n. No matter how big N is, it’s always possible to find a larger n.

For example, the function

  has removable discontinuous at 1, 2 and 3.

If assuming partitions of [a, b] into n subintervals of equal width (b-a)/n.

When ti* ≠ 1, 2, or 3,

When ti* = 1, 2, and 3,  there exists at most 6 subintervals that it is possible to choose a sample point ti* at discontinuous points.

Hence

Therefore, functions with finitely many removable discontinuities are integrable.

——–

math 101 Assignment 1 Q3

f(x)=x²ln(x)

1. What is the domain of the function?
2. Does this function have any intercepts with the axis?
3. What are the turning points?
4. What is the x value of the point of inflection?
5. Sketch the graph.

Continue reading →

A person flies a kite on the main mall. The kite rises at a rate of 2 meters per second. Suppose the horizontal distance between the person and the kite is always 6m, how fast must he release the string when the length of the string is 10 meters?

——

To solve this question, we let the height of the kite be H and the length of the string be L.

The relation between H and L is:  H² + 6² = L² . So when L is 10 m, the height of the kite is 8m.

Then, we differentiate both side of the equation above.

2H × H’(t) + 0 = 2L × L’(t)

H × H’(t) = L × L’(t)

L’(t) = H × H’(t) ÷ L

We are given the rising rate of the kite is 2 m/s, this means that H’(t)=2.

So, L’(t) = 8 × 2 ÷ 10 = 8/5 .

First of all, we need to understand that the function of the temperature is continuous. In other words, the temperature changes gradually, either increasing or decreasing. It’s impossible for a 100 degree Celsius object become 0 degree Celsius at the next moment. The energy must be absorbed or released continuously, or a little by a little. Thus, all values on the graph of the temperature are connected without any jumps.

Since the temperature is changing gradually from two random points, position a to position b, we are able to find two places x in each side of the interval a and b and its temperature is between T(a) and T(b). The distance between a-x and b-x must be equal, because the temperature changes at the same rate. This means that these two places x are opposite to each other. The line of two x also passes through the center of the circle. Therefore, the temperatures of two antipodal points are the same.

Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!

The distance of walking can be represented by a function. Suppose a person is walking at a constant speed, then the growth rate of the distance he travels is a constant number. Since the displacement per unit time are all the same, the graph of this function (distance versus time) will be a straight line. So there is no horizontal asymptotes.

Suppose I’m eating a box of cookies. At the first time I eat 1 cookie, and ½ at the second time. And every time afterwards, I’ll eat half amount of the previous.

The amount of cookies I eat every time is a sequence made by a list of numbers. This sequence converges to 0, because I eat less and less cookies.

The total amount of cookies I eat is a series, which sums up how much I ate. This series converges because it is a geometric series with a ratio of ½. And series ∑(0.5)^n converges to 2.