Group Member:
Alphonse Wang: 47168166
Chenming Hu: 17973165
Qiwei Liang: 33196153
Yuqi Liu: 44616167

Group Member:
Alphonse Wang: 47168166
Chenming Hu: 17973165
Qiwei Liang: 33196153
Yuqi Liu: 44616167
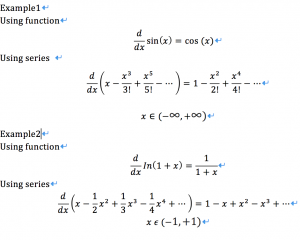

Group Member:
Alphonse Wang: 47168166
Chenming Hu: 17973165
Qiwei Liang: 33196153
Yuqi Liu: 44616167
Integration: Integration is a kind of operation which calculates the area between the curve and x-axis in a given range. To integrate, we basically need a function and two x values which is the range of integration. Without these elements, it’s hard to do the integration.
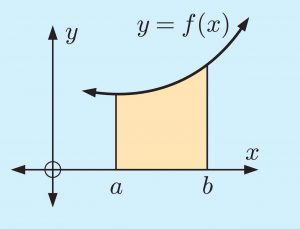 figure 1
figure 1
Take figure1 as an example, the integration of this graph is the yellow area. The formula of this area is abf(x)dx , as the formula shows,we need a value for a, b and the function of f(x). The integration will get an exact value of the area. When we integrate the function, the constant c does not matter in the formula. The result of formula will use F(b)-F(a) where F(x) is the anti differentiation of f(x). When F(b) minus F(a), the constant c will cancel out. We can also think about it by thinking about the graph. Adding c means the graph of anti differentiation function will increase by c. F(b) and F(a) will both increase by c. The difference will not change.
Anti differentiation: The process of solving for antiderivatives is called anti differentiation and its opposite operation is called differentiation. We assume that F(x)’=f(x), thus, f(x)dx=F(x). However, that is not true because it is incomplete. As we can see it clearly in this illustration,
when we get an f(x), and do the antidifferentiation for f(x), we can find a lot of function satisfy this equation; as the diagram illustrates, we can sketch countless curve with the same slope at every same point. So we can summarize that if we do the antidifferentiation for f(x), we can get an assemble of new function recorded by F(x)+C, C is a real number. For instance, given a function such as f(x)=x^2, do the antidifferentiation, then we can get the original function 1/3*x3+C.
Differences: The major difference between “integration” and “anti differentiation” is that the result of integration is a number, but the result of anti differentiation is an assemble of function, that means

when we want to do the integration, anti differentiation is a necessary step of it. As we introduced before, integration is the area of f(x) in a given interval, but in the diagram of F(x)+C, it illustrate the change value of F(x) in the given interval. However, we can easily find that no matter what the value of C, the change value in the given interval is always the same, because of the same slope all the time of F(x)+C. As the example before, f(x)=x^2, first we do the anti differentiation for it, we get F(x)+C, if we want the integration in [-1,1], we substitute -1 and 1 to the function, we get F(1)+C-F(-1)-C, no matter what the value of C, the result can be all the same.
Why confused:Why students always confuse about integration and anti differentiation?
It’s easy to mix these two operations together because these two operations will operation the original function in the same way. When students calculate about the function, they will look at the function and just calculate the value, they don’t think about what’s the operation, integration or anti differentiation. Obviously, the result is different. However, the process will confuse. Integration should calculate about the anti differentiation F(x) to get F(a) and F(b). Anti differentiation will get the similar result of the second step of integration, only difference by c. I think that’s the reason why students always confuse about these two operations.
Yuqi Liu 44616167
Alphonse Wang 47168166
Chenming Hu 17973165
Qiwei Liang 33195453
Chenming Hu 1797365 / Qiwei Liang 33196163
Alphonse Wang 47168166 / Yuqi Liu 44616167
Motivation of Integration
Before 370 BC, ancient Creek Astronomer Eudoxus had an idea to find the specific areas and volumes by breaking them up into small pieces of area for which the area and volume was known. This method was further developed and employed by Archimedes in 3rd century BC and used to calculate approximation to the area of a circle. And over last thousand years, the way of using integral has been promoted by lots of scientist. During these thousand years’ promotion, a famous scientist Isaac Newton used a small vertical bar above a variable to indicate integration. However, the box notation was difficult for printers to reproduce, so these notations were not widely adopted. Finally, in 1675 Gottfried Leibniz create the modern notation for the indefinite integral.
Today ‘Integration’ as a term is widely applicated as different meaning in different disciplines such as Sociology, economy and Engineering. Etc. In mathematics, ‘integration’ usually is represented as ‘integral’ which utilize a function to assign number to represent area, volume and other concepts by breaking them up into an infinite number of division. For example, using integrals to find out the different value. For some functions, some parts are positive and above the x-axis, and some parts are negative which are below the x-axis. When we try to figure out the average of these values, we can use the graph, and add the positive areas and negative areas together and find out the difference between two values. Using graph can give a visual feeling directly and help researchers.
Moreover, people use ‘integral’ to determine the area under a curve and do the data analyzing in many field, typically, in physics. In physics, people always use a function to represent the relationship between speed and time. From this kind of function, we are not only looking the changing of the speed, but also the area under the curve, which can represent the displacement of the object in this time period. When we analyze the function, we can find out the moving state and position state of this object. What is more, when the function is about the acceleration and time. The area under the curve is about the speed, and by analyzing the acceleration and speed of the object, we can figure out the position. Therefore, the data can help us find more data. Both of these two examples relate the integral and the real life together, and it shows the integrals exist in many fields.
All in all, integration has already connected with our life and acadamic study. So hopefully, right now you have the motivation to learn ‘INTEGRATION’.
In the third problem, first two small problems are easy. The theory used is just the basic definition of the limitation. In (c) problem, we should rethink about the definition and figure out what conditions do we have and what is needed to prove the (c) problem. Also, when you do this problem, you should not trap in the answer of (a) and (b). The condition in the (a) should be linked with the condition of (b). Besides, the transfer is also important in this problem.
Sequences are the combine of infinite terms with a general term. Series is the sum of the sequences.
The limit is like there is a wall, we can close to the wall as near as possible, but we cannot get on it and get over it. The sequences converge when the sequence {an} has a unique limit. It diverges when there is no limit of the sequence. Just like there a line of people which is limit in the wall and they can get as close as possible to the wall. If there is no wall and people can go anywhere, then that’s divergent. If they are limited in the wall, then it’s convergent. For example, {1/n} is convergent because it can get very close to zero, but it cannot equal to zero and smaller than zero.
Series is that the sum of the infinite terms is eventually close to a number. You can image that there are people lie on the ground, the height of them is getting shorter and shorter. As the added height is adding is getting smaller and smaller. The sum of their height will be very close to a number. If there is a number that the sum of the sequence is converge to, then the series is convergent. For example,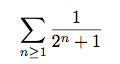 is convergent because the term is getting smaller and smaller and almost zero. So there is a result of this series, so it’s convergent.
is convergent because the term is getting smaller and smaller and almost zero. So there is a result of this series, so it’s convergent.
Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!