Sequences are the combine of infinite terms with a general term. Series is the sum of the sequences.
The limit is like there is a wall, we can close to the wall as near as possible, but we cannot get on it and get over it. The sequences converge when the sequence {an} has a unique limit. It diverges when there is no limit of the sequence. Just like there a line of people which is limit in the wall and they can get as close as possible to the wall. If there is no wall and people can go anywhere, then that’s divergent. If they are limited in the wall, then it’s convergent. For example, {1/n} is convergent because it can get very close to zero, but it cannot equal to zero and smaller than zero.
Series is that the sum of the infinite terms is eventually close to a number. You can image that there are people lie on the ground, the height of them is getting shorter and shorter. As the added height is adding is getting smaller and smaller. The sum of their height will be very close to a number. If there is a number that the sum of the sequence is converge to, then the series is convergent. For example,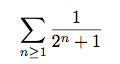
is convergent because the term is getting smaller and smaller and almost zero. So there is a result of this series, so it’s convergent.