Tong Cui (Chelsea)

The simplest way to answer this is by saying that integration is a way of adding small slices or small parts to find the whole. And it can be used to find areas, volumes, and central points of many things. So, how can we use those slices to find the area or volume? Imagine that we have a glass and tap water. Integration is like filling the glass from a tap. Adding up the little bits of water to the bucket gives us the volume of water in the bucket.

In more mathematical way, if we are being asked to find the area of a triangle or a circle or a square, it’s easy since we already know the formula of those shapes. But, imagine if we are being asked to find area of irregular shapes, e.g an irregular curve.

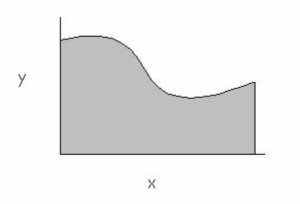
A good starting point will be to draw rectangles in the area of this shape because as we said before, we already knew how to calculate the area of the basic shapes.
Then, we can calculate the area of both rectangles and add them together. However, to be noted, the problem with this method is that it’s only a rough approximation of the area (not the factual area).

So, the solution is to make the rectangles narrower as you can see in the picture below.

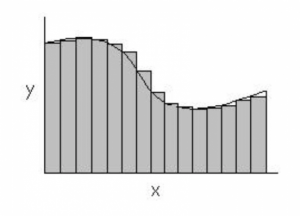
As the rectangles get narrower, the approximation of the area will be more precise, but keep in mind that it is still not the factual area, because we will always have either underestimate or overestimate value, depending on which point (the left point or the right point of the rectangle width) was chosen to make the calculation. One aspect to consider is that when the curve gets more irregular the approximation of the area will be more difficult to calculate.

Just like the examples that show previously, integration could be applied widely no matter in real life or abstract math problems. In order to find the most efficient solution, based on the concept of simplification, we connect some scattered parts to form a valuable whole through a particular way, which is the main idea of integration.

Group members:
Clarissa Audrey 51844165
Mariana Paspuel 44069169
Violet Ye 52433166
Chelsea (Tong Cui) 31032162