Provide a recurrence relation for the quantity described in each of the following problems (these can be the basis for a dynamic programming algorithm to solve these problems; we will discuss this technique in class this week). Note that recurrence relations can be used to describe any mathematical function that is defined in terms of its values for smaller arguments. They are not only used to determine algorithm runtimes!
- Let G = (V, E) be an undirected graph with n nodes. A subset W of the nodes is called an independent set if no two elements of W are joined by an edge in G. That is, if we were to delete all of the vertices of G that are not in W, as well as all the edges connected to them, we would be left with |W| isolated vertices and not a single edge. For instance, in the graph shown below, the nodes with weights 2, 6 and 6 form an independent set. So do the nodes with weights 2 and 3. However the nodes with weights 2, 8 and 3 are NOT an independent set, because there is an edge between the nodes with weights 2 and 8.
Finding large independent sets is difficult in general, but it can be done efficiently if the graph is simple enough. Let us call the graph G a path if its nodes can be written as v0, v1, …, vn-1 with an edge between vi and vj if and only if the numbers i and j are consecutive. With each node vi we associate a positive integer weight wi. For example, in the following path, the weights are the numbers drawn inside the nodes (we have not numbered the nodes themselves).

Define recurrence relations for
- With[i]: the maximum sum we can obtain using non-consecutive elements from v0, …, vi, including the element vi in the sum.
- Without[i]: the maximum sum we can obtain using non-consecutive elements from v0, …, vi, without including the element vi in the sum.
- There are many sunny Spring days in Vancouver. Unfortunately, this year, it is raining on the day of the CSSS boat cruise and dinner. The CSSS president decides to rebook the cruise for another day, and needs to contact everybody who has made reservations. Luckily, every student made his/her reservation by talking to another student who had already made his/hers. That is, the students who have reservations for the cruise form a tree, whose root is the CSSS president!
To notify everyone of the postponement, the CSSS president first calls each of the students who bought their tickets directly from him/her, one at a time (his/her “children”). As soon as one of these students has been notified, he/she can then notify all of his/her “children”.
We can picture this process as being divided into rounds. In one round, each person who has already learned of the postponement can call one of his/her children. The number of rounds it takes for everyone to be notified depends on the sequence in which each person makes their phone calls. For instance, in the following figure, it will take only two rounds if A calls B first, but three rounds if A starts by calling D (note that A can not call C directly).
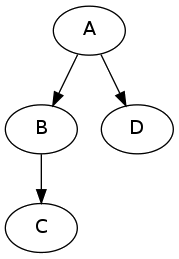
Write a recurrence relation for R(N), the minimum number of rounds needed to inform all descendants of a node N.
- As some of you know well, and others of you may be interested to learn, a number of languages (including Chinese and Janapese) are written without spaces between the words. Consequently, software that works with text written in these languages must address the word segmentation problem: inferring likely boundaries between consecutive words in the text. If English were written without spaces, the analogous problem would consist of taking a string like “meetateight” and deciding that the best segmentation is “meet at eight” (and not “me et at eight”, or “meet ate ight”, or any of the huge number of even less plausible alternatives). How could we automate this process?
A simple approach that is at least reasonably effective is to find a segmentation that simply maximizes the cumulative “quality” of its individual constituent words. Thus, suppose you are given a black box that for any string of letters x = x0, x1, …, xk will return a number Q(x). This number can be either positive or negative; larger numbers correspond to more plausible English words. So Q(me) would be positive, while Q(ght) would be negative.
Given a long string of letters y = y0, y1, …, yn-1, a segmentation of y is a partition of its letters into contiguous blocks of letters; each block corresponds to a word in the segmentation. The total quality of a segmentation is determined by adding up the qualities of each of its blocks. So we would get the right answer for the problem above provided that Q(meet) + Q(at) + Q(eight) was greater than the total quality of any other segmentation of the string.
Give a recurrence relation for TQ(i): the maximum total quality of any segmentation of the letters y0, y1, …, yi. Hint: look for the position of the first letter of the current “word”.