Tutorial #5 solutions – CPSC 320 2017W2

- Sometimes. Here’s a true instance:
```
            m1: w1 w2   w1: m1 m2
	    m2: w2 w1   w2: m2 m1
```
  and here is a false instance:
```
            m1: w2 w3 w1  w1: m2 m3 m1
	    m2: w3 w1 w2  w2: m3 m1 m2
	    m3: w1 w2 w3  w3: m1 m2 m3
```
- Assuming the graph is finite, the answer is NEVER. First, here is a false instance: A→B. We can in fact prove that it’s not possible for the out-degree of every vertex to exceed its in-degree by contradiction. Suppose that was the case. Then the sum of the out-degrees is larger than the sum of the in-degrees, which is impossible as the two sums must be the same (every edge has two endpoints, and contributes to the in-degree of one vertex and the out-degree of another vertex).
- Note that the reduction is correct exactly when it produces a correct solution for every legal instance of EDP. So, the counterexample MUST be an instance of EDP. It is NOT an instance of NBP or anything else.The part of the reduction that went wrong is the fact that we made the bandwidth of edges leading to the distribution point analogues in NBP just 1. That means that each distribution point can only send out 1 byte per second. But, each distribution point is supposed to be allowed to be the source of multiple paths. So, that’s our target: make a distribution point that is the source of multiple paths and show that the reduction fails on it.Here’s the smallest graph that accomplishes this. It should work as our counterexample:
  
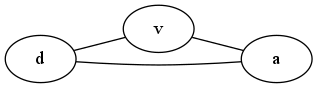
  Note that the correct solution to this problem is 2, using the path that goes through v plus the one that goes direct (which uses all edges; so, there’s no possibility of a higher value!).
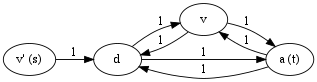
- Normally, we’d ask first for the NBP instance’s solution and then for the solution the reduction produces from that, but since the reduction just produces whatever NBP produces, we go straight for the final, incorrect solution.The incorrect solution is 1. How do we achieve 1? Many ways, but one is to use the path v’ → d → a. Why can’t we achieve more? The source has only one edge with weight 1 leading out of it; so, we cannot possibly do better than sending one byte out of it, unfortunately.Remember that when you check correctness of a reduction, you should assume that you get a correct (but otherwise arbitrary) solution to the underlying problem. I.e., you have a correct NBP solver accessible to your reduction, but you cannot say anything about how it works except that it is correct.
- The correct solution is 2 by the paths that include and exclude v. Note that with infinite weight coming out of v’, we would indeed discover this in the NBP instance.
- The idea behind the algorithm is simple: since a guard needs to cover the precious object at the leftmost position, we might as well place him/her as far to the right as possible (maybe it will then cover other objects as well). Then we repeat the procedure with the next leftmost unguarded treasure. This can be written up formally as follows:
```
    G ← { }
    Sort X in increasing order
    
    pos ← 0
    While (pos < length[X]) do
        //
        // Place a guard as far right as possible to cover X[pos]
        //
        x ← X[pos] + d
        add x to G
    
        //
        // Skip the other treasures this guard covers
        //
        do
            pos ← pos + 1
        while (pos < length[X] and X[pos] ≤ x + d)
    
    Return G
```
- This algorithm runs in O(n log n) time, because of the time required to sort the array of positions.
- Here is a more or less complete proof of correctness (you weren’t expected to come up with this during the tutorial).
  First we show that there is an optimal solution whose leftmost guard is placed at the same location as the leftmost guard returned by our algorithm.Suppose that G^* is an optimal solution to the guarding problem. Let l be the position of the leftmost painting, x be the first position where our algorithm places a guard (that is, x = l + d), and x^* be the position of the leftmost guard in G^*.Clearly x^* ≤ x, since otherwise G^* would not cover the leftmost painting. The guard placed at x covers every painting in the range l ... x+d. Consider an arbitrary painting covered by the guard placed at x^*. Its position is ≥ l (the leftmost painting) and \le x^* + d ≤ x + d. Hence it is also covered by a guard placed at x.
  
  Therefore every painting covered by a guard at x^* is also covered by a guard at x, which means that G^* - { x^* } + { x } covers all the paintings. It contains the same number of guards as G^*, and hence it is an optimal solution that contains x.