Summary

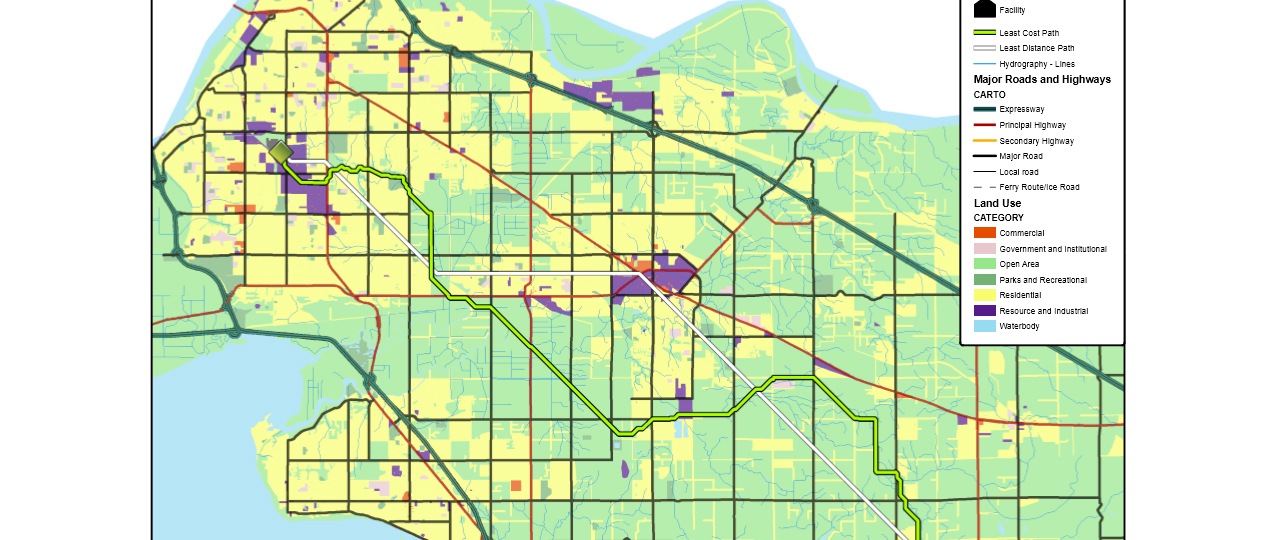
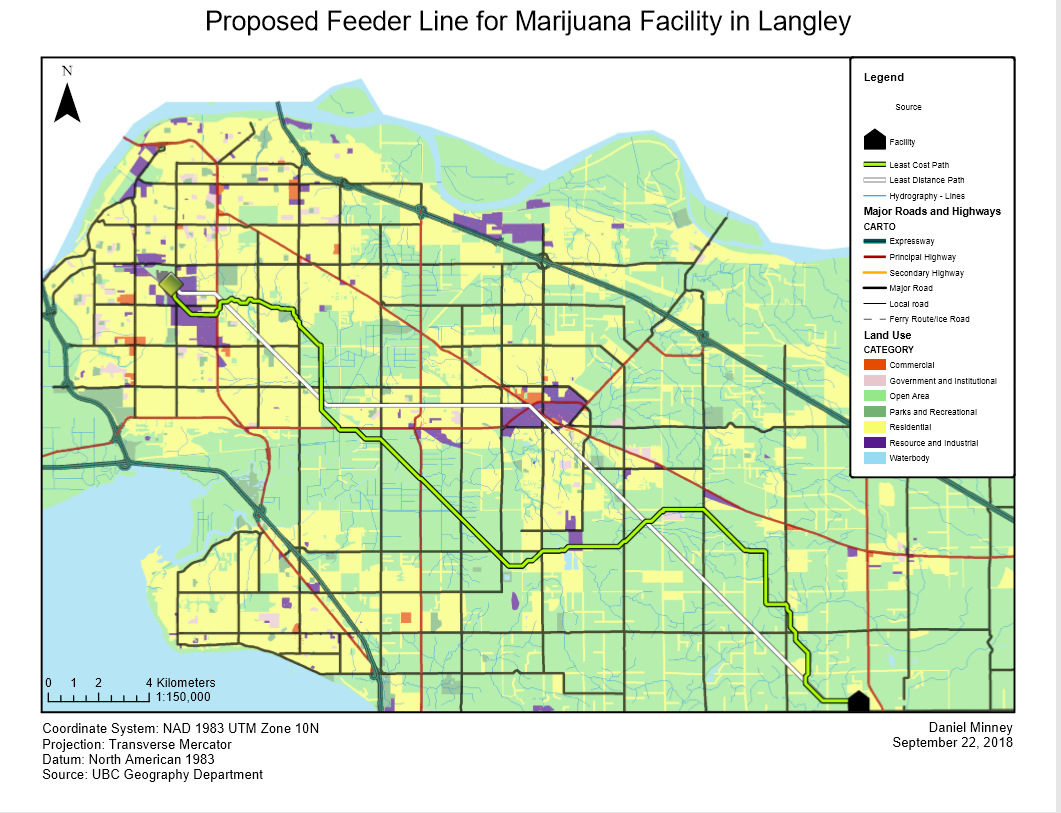
Using data provided by the UBC Geography Department, a theoretical proposed feeder line was created using the least cost path tool, where different weights were given to each cell depending on their resistance. A shortest-path route was also created as a comparison.

The shortest-path provides the shortest possible route between the source transformer station and the proposed facility. While this is the shortest route in terms of distance, it is not the most cost-effective path as it is likely crossing land which would be expensive to build on.

The least-cost path provides an alternative route which considers the cost of crossing certain land. By using land use as delineated by the city, and values assigned to each land use, an alternative route can be constructed that while expands over a further distance, crosses land of lesser cost, and ultimately providing a cheaper route from the source transformer station to the proposed facility.

The length of the shortest-path route is 34.16 km, whereas the length of the least-cost path is 41.48 km. However, the total cost for the shortest-path route is $1,997,750, whereas the total cost for the least-cost path is $275,346. This displays the effectiveness of the least-cost path tool.

The length of the shortest-path route is 34.16 km, whereas the length of the least-cost path is 41.48 km. However, the total cost for the shortest-path route is $1,997,750, whereas the total cost for the least-cost path is $275,346. This displays the effectiveness of the least-cost path tool.

Other factors such as schools and farmland were not considered in the least-cost path. A solution that preserves farmland would complicate the problem even further. “Open area” land use covers a very large area, and Langley has a significant amount of farmland. Friction values for farmland would have a value of NoData, meaning that it is an absolute barrier. The route of the least-cost path would be affected, likely increasing the distance and complexity. To create a more nuanced cost surface, we could add an additional land use area that contains a 500 meter buffer around each school, and a value of NoData would be set for this area. The result would be a least-cost path that stays at least 500 meters away from schools. Currently, there are four schools within 500 m of the least-cost path, and twenty one schools within 500 m of the least-distance path.