Convergent sequence has a real number as its limit, which means it sufficiently close to that real number. Like the picture below:
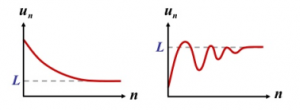
Let’s explain it by using some examples.
Ex.1
A sequence is an = {2, 2.01, 2.001, 2.0001, 2.00001, ……}. When n become as large as we want or we can say it arbitrary large, we will find that this sequence an is getting as close as we want or approach to 2. Since it is a real number, it means the sequence an is sufficiently close to 2, so an is a convergent sequence and it converges to 2.
Ex.2
A sequence is bn = {7, 8.5, 7.2, 8.3, 7.8, 8.1, 7.97, ……}. When n become arbitrary large, we will find that this sequence bn bounds and approach to 8 from above and below. Since it is a real number, it means the sequence bn is a convergent sequence and it converges to 8.
Here is the graph of divergent sequence:
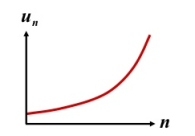
Divergent sequence does not have a real number as it’s limit, it just continue to get further and further apart which means away from 0 and any real number.
Ex.3
A sequence is cn = {1, 2, 3, 4, 5, 6, ……}. When n become arbitrary large, we will find that this sequence cn does not get close to any number. Since the limit is endless we can say it is infinity, it means the limit of the sequence cn does not exist, so cn is a divergent sequence.
Now let’s talk about series:
In mathematics, series is the sum of a sequence which contains n numbers. We use Σn≥1 to represent it.
Here is an image to show what are converge series and diverge series:
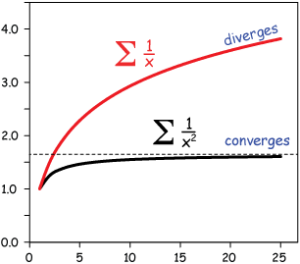
If we want a series which converges , the partial sums of its sequence has to have a real number as its limit, which means it sufficiently close to that real number.
Ex.4
A series is Σn≥1 ½n = {½ + ¼ + 1⁄8 + 1⁄16 + ……}. When the series add as many numbers as we want we will find that the number is REALLY small and the term become small very quickly. However, the series become large very slowly and getting close to 1. End up this series become sufficiently close to 1 which is a really number, so Σn≥1½n is a convergent series and it converges to 1.
If the series is divergent , the partial sums of its sequence does not have a real number as its limit, which means the limit of the series does not exist. The series just continue to get farther and farther apart away from real number,
Ex.5
A series is Σn≥1 1⁄n = {1+ ½ + ⅓ + 1⁄4 + 1⁄5 + ……}. When the series add as many numbers as we want we will find that the top values are equal or greater than the bottom ones, thus the sum becomes very large. End up this series does not close to any real number which means infinity and the limit of this series does not exist, so Σn≥1 1⁄n is a divergent series.
Monthly Archives: September 2016
test
Hello world!
Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!