Irving Langmuir (1881 Jan 13 – 1957 Aug 16) once derived a neat equation that describes the evaporation of a liquid. And he used an astonishingly elegant argument to get it.
We begin to follow Langmuir’s logical path by assuming that we have a body of some mono-molecular liquid, such as water or ethyl alcohol, with a suitable atmosphere of gas, whose pressure prevents the liquid from boiling, lying atop it. We also assume that the gas contains a certain amount of the liquid’s vapor, which exerts a partial pressure upon the gas-liquid interface. We want to calculate the rate at which the molecules of the vapor strike a small area of the interface.
Establish a minuscule area dA on the interface and establish two angular coordinates. We measure the polar angle θ with respect to a line drawn perpendicular to dA and the azimuthal angle φ with respect to an arbitrary circle lying parallel to dA. Consider only those vapor molecules that float arbitrarily close to the interface and that have velocities v with speeds in the range between v and v+dv oriented in directions whose angular coordinates lie between θ and θ+dθ and between φ and φ+dφ.
Define a minuscule interval of time dt such that vdt is very much shorter than the mean free path of the vapor molecules, thereby ensuring that only a negligible number of molecules get deflected by collisions before they can reach the interface. We thus have a set of vapor molecules contained within a skewed cylinder of cross section dA and length vdt (whose direction makes an angle θ with the normal to the interface) which strike the interface in the interval dt. That cylinder contains a volume dA(vdt)cosθ and contains vapor molecules of the designated speed in the density f(v)d3v. The product of multiplying those two numbers together tells us how many vapor molecules strike the given area of the interface in the given elapse of time.
If we divide that product by dA and dt, we get
(Eq’n 1)
the rate at which vapor molecules with velocities between v and v+dv strike a unit area of the interface. To get the total rate at which vapor molecules strike a unit area of the interface we must integrate that function over all relevant velocities, so we get
(Eq’n 2)
in which v+ represents vcosθ>0; those vapor molecules for which v+<0 won’t hit the interface, so we dismiss them from our calculation as irrelevant.
We want to carry out that integration over the appropriate region of velocity space using the same angular coordinates that we established for location space. The element of volume in that space comes out as
(Eq’n 3)
in which dΩ represents the minuscule solid angle on a spherical shell of radius v. We thus get Equation 2 as
(Eq’n 4)
In the last line of that equation n represents the density of the vapor molecules and the barred vee represents the average speed of the molecules (which we calculate explicitly in the appendix below). Using the ideal gas law in the form p=nkT to substitute for n in Equation 4 and using the explicit calculation of the average speed in terms of the temperature gives us
(Eq’n 5)
If we multiply that equation by the mass of each vapor molecule, we get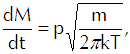
(Eq’n 6)
the flux of vapor molecules in kilograms per square meter per second onto the interface. Having thus tacitly assumed the use of the MKS system of units, we must now require that we express pressure in newtons per square meter, molecular mass in kilograms, and thermal energy in joules.
Now we come to Langmuir’s genius-level flash of inspiration. He conceived the liquid as a gas in which the vapor was dispersed in accordance with the liquid’s vapor pressure. Thus, for example, he would conceive gasoline as a gas of substance X with gasoline vapor dispersed within it. He could then use Equation 6 to calculate the rate at which the vapor would strike the interface from the liquid side. Because any molecule that strikes the interface passes through it, that calculation represents a flux of vapor from the liquid. If we then subtract from that calculation the flux of vapor coming into the liquid from the gas, we get Langmuir’s evaporation equation,
(Eq’n 7)
In that equation pv represents the vapor pressure of the liquid and pp represents the partial pressure of the vapor in the gas. We can see that if pv exceeds pp, we will have net evaporation and that if pp exceeds pv, the net mass flux comes out as a negative number and we thus have net condensation.
Appendix: Average Molecular Speed in a Gas
In deriving Langmuir’s evaporation formula we had to use the average speed of a molecule in a gas. We have a standard calculation of that average based James Clerk Maxwell’s theory of the distribution of particle velocities in an ideal dilute gas. We start by equating the product of the particle density in the gas and the average particle speed to the integral over all of velocity space of the product of a speed with the probability of a particle having that speed,
(Eq’n A-1)
In that equation we have the mean density of molecules with center-of-mass speeds between v and v+dv as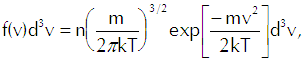
(Eq’n A-2)
which reflects the Maxwellian distribution of speeds among the molecules. For any given speed we must integrate over a spherical shell in velocity space that contains all velocities that correspond to that speed, so we have the differential volume element as![]()
(Eq’n A-3)
We divide Equation A-1 by the particle density and make the necessary substitutions to get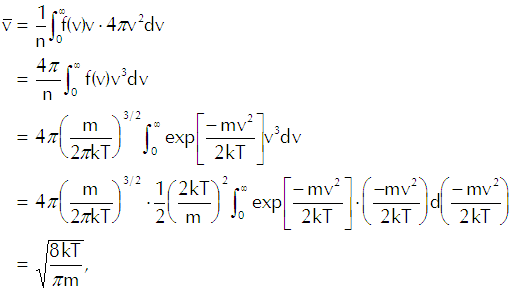
(Eq’n A-4)
which gives us the result that we use in our derivation of Langmuir’s evaporation equation.

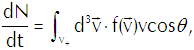
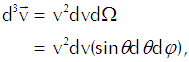
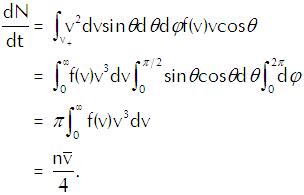
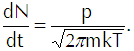
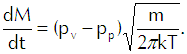
this subject isn’t so unknown to me, so i enjoy reading it. thanks. lista de email lista de email lista de email lista de email lista de email
Hey Jun,
As I try and wrap my brain around simplifying this down to a few variables and a constant, I’m struggling with the ideal gas law and partial and vapor pressures, just not my gig. Do you have formula that will accept the variables we currently measure?
Where is the source?