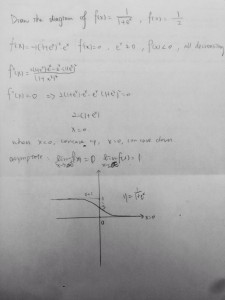
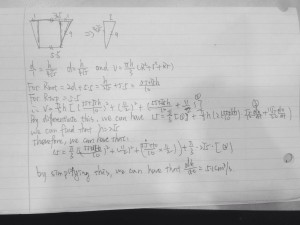By searching through wikipedia, I’ve got An analytic function is a function that its Taylor series at any point x_0 in its domain converges to the function itself for x of x_0. It means that if a function is analytic at c, it can be expanded to the Taylor series centered at C, like e^{x}, it can be expanded analytically. Therefore, the differences between Analytic function and infinitely differentiable is that the previous one can expand into power series representation but not every infinitely differentiable function can be expanded into every x.
Midterm Review
After reviewing the midterm that I have already taken in February, I generalize following details that I still need to improve.
- Calculation of Integration, which means I’m not familiar enough to solving the integration problem, not merely lacks of practices but generalize the types of integration problem.
- Way of approaching problem, even though I was done a so-so job for the questions expect #1, but after reviewing the steps that provided, I am still not enough for mathematical logic.
- Managing time; I’m not reasonably manage my time during exam, which caused I don’t have enough time to review the whole exam sheet.
Tips of Integration Substitution
1, When approaching a new question, even though it was hard, we can firstly have some tries, try some terms that represented in the question.
2, We can simplify the function before we start doing substitute, if it can.
3. Try to remember some of the important trigonometric transformation, it might help when we have no clue.
Proof of Integrable
The question told us that f(t) has removale point when t=1,2,3,4…. and the general function discontinuous. However, back to the definition of integrade, its general idea is about divide part of a function into infinitely pieces and add those all together by select a certain point on the width you choose; thinking of this, we can apply that idea into this question, which we can choose that certain point ti without endpoints defined. Therefore, we can say that it is integrable.
Sketching Graph
Coffee cup question
Intermediate Value Theorem of Circle
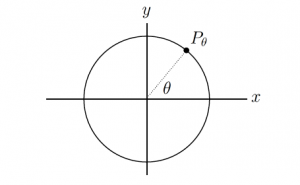
We’ve worked on the Intermediate Value Theorem (I’ll call it IVT in rest of my article) recently, according to the image, here goes a problem about IVT application, its mainly idea is to prove there exist a antipodal of P0
When convincing people who has no background knowledge about IVT, we can use the airplane flying trajectory to clarify:
When a plane have to fly from Southern Hemisphere to Northern Hemisphere like Australia to Canada, no matter what trajectory it would follow, that plane will definitely fly through the Equator. When drawing a picture of what I’ve presented, the airplane’s trajectory will go across the equator no matter what.
We can suppose that Australia is point a and Canada is point c, which correspond to interval (a, b), it is continuous. When connecting it to a xy-axis(y is the equator) graph, that interval can have a value interval (f(a), f(b)), according to this, the cross point of flying trajectory and equator is the c in interval (a, b), it has a value f(c)=0 and in the interval of (f(a), f(b)).
Mathematically speaking, the IVT definition is:
When a function is continuous, we can pick a c in the interval of [a, b], and there exists a f(c)=L in the interval of [f(a), f(b)].
Consideration of a sequence, a series and a function
Recently, we’ve worked on some problems about sequence converges and series converges. For certainty, there are some expressive sequences and series that I want to discuss.
We say that {an} is Cauchy if an and am are arbitrarily close to each other provided n and m are sufficiently large.
This is how Professor Leung described in our pre-reading assignment. Cauchy sequence is a converge sequence which also has a converge subsequence. We can find that everywhere, we describing a diagram, composing a stock curve etc. Cauchy sequence applies in every part of our life especially in software and finance.
When considering a series, I will definitely link it with the annual saving rates of commercial bank. Longer the time you save your money in it, higher the saving rates you can get, just like a adding series.
Every time we playing sport like basketball, we could probably found out that after we throwing the basketball, flying trajectory was like a perfect curve function, which has a horizontal asymptote.
Hello world!
Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!