Bai Jingwen(Vivienne): 55932164,Li Mengmeng(Astrid): 59418160,Lu Xuechun : 41519166,Xu Cuishan (Tracey ):32182164

Bai Jingwen(Vivienne): 55932164,Li Mengmeng(Astrid): 59418160,Lu Xuechun : 41519166,Xu Cuishan (Tracey ):32182164



Bai Jingwen(Vivienne): 55932164,Li Mengmeng(Astrid): 59418160,Lu Xuechun : 41519166,Xu Cuishan (Tracey ):32182164




Bai Jingwen(Vivienne): 55932164,Li Mengmeng(Astrid): 59418160,Lu Xuechun : 41519166,Xu Cuishan (Tracey ):32182164
Integration and anti differentiation are commonly conflated since it’s generally misunderstood that they are both the inverse of differentiation. However, they are totally different in their exact definitions, despite that they are indeed connected in some way. Integration is the process of calculating integrals, i.e. the area under a fixed curve, which is a number. Whereas antidifferentiation is the process of finding the antiderivatives of a function, which are a number of functions. Comparing these two vague definitions, it can be assumed that antidifferentiation is not equal to integration.
What is anti-differentiation ?
Antidifferentiation can be understood as the inverse of differentiation.
For a function f(x), the antiderivative (primitive function) of this function, ![]() , are a group of functions F(x)+C that satisfies the derivative of this group functions is f(x).
, are a group of functions F(x)+C that satisfies the derivative of this group functions is f(x). ![]() . So the antiderivative of f(x) is not unique.
. So the antiderivative of f(x) is not unique.
example : 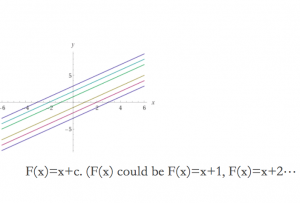
What is integration?
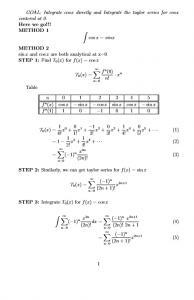
For integration, integral can be defined by Riemann Sum.
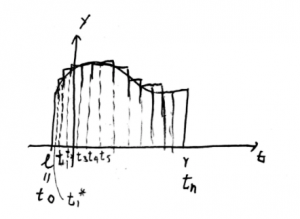
let f(t) de defined on a closed interval [a, b] and divide [a, b] into n subintervals
with the same t value, choose a sample point ti* within [ti-1,ti], so that the area of one rectangles is ![]() ,so the area of these rectangles is
,so the area of these rectangles is ![]() .
.
Given a continuous function f(x) and an interval [a, b], the meaning of integral ![]() is the area of curve trapezoid formed by function f(x), x=a , x=b and x-axis in x-y plane (as illustrated in this picture). So integration is a certain real number.
is the area of curve trapezoid formed by function f(x), x=a , x=b and x-axis in x-y plane (as illustrated in this picture). So integration is a certain real number.
What is the connection between integration and antidifferentiation ?
Integration and antidifferentiation are correlated by Fundamental Theorem of Calculus (FTC) since an integral can be evaluated by using antiderivatives. As FTC2 said, if G(x) is an antiderivative of f(x), then we have,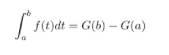
This means to evaluate the integral of continuous function f(x) defined on [a, b], we just need to take antiderivative of the function. In this way, after finding an antiderivative of a function, we can simply plug in x=b and x=a, and subtract these two values. Hence it is where they are connected that antidifferentiation can be used in calculating integrals.
Why students commonly mistake “Integration”& “Antiderivation”?
Motivation of integration
(Mengmeng Li (Astrid), XuEchun Lu (Leonie), Cuishan Xu (Tracey), Jingwen Bai (Vivienne ))
Integration is used to calculate the area under a certain line, curve or the area which covered by an image in math. Like calculating the area for a piece of leaf. When we doing integration, we tear the leaf to a lot small rectangle strips whose area can be easily calculated. Approximately, the sum area of strips is area of the leaf. Moreover, integration can be used to calculate a curve’s length by regarding the curve to a lot short straight lines. As an important math concept, not only can it be applied in math to calculate area and length and in physics to calculate the movement about one subject, it can also be applied in our daily life observation.
It was a sunny day, our team was eating in the Orchard Common, and we found it that there is a big irregular hole (the depth varies) on the table. Everyone wanted to know the exact volume of plastic material do the staff in dining hall need to fill this hole. At the same time, Tracey was eating French Fries, she was thinking “Oh why not fill the hole with fries so as to calculate the volume by calculating the volume of fries?”. It is noted that French Fries has the same length and width but different height and the height of fries could be cut to fit the depth of the hole.
To calculate the volume of the hole, firstly we put a cardboard under the hole so as to accommodate the fries in case they fell on the ground. And then the filling started from the side of the hole. We put fries into the hole and compared the height between the fries and the depth of the hole. The extra parts were eaten by Tracey. And repeat the procedure. Finally, the irregular hole was full. Now Tracey put all the fries from the hole on the plate in order. Vivienne yelled that, it is the volume of the hole, we can calculate the total volume by adding the volume of fries one by one. It’s obvious that the volumes of different fries are easy to calculate once knowing the fixed length & width and the various heights. This is a normal case in daily life.
Like the volume of a hole we saw in our dining hall. We can separate it in small pieces and get the hole’s volume by calculating every small piece’ volume. The method is just the basic content of integration. Integration, in total, is a method to make complicate things easier by making it smaller. Thinking of puzzles, every little piece of puzzle can be connected together to a masterpiece. By using the way to integrate something, we can approximately get the value which is hard to get straightly.
When you think about this question, you need to think about g(x) get close to g(a) thus making f(g(x)) close enough to f(g(a)).
For example, think about a point with a ball. If x closes enough to a, the ball contain g(x) to g(a) will close to be a point. So that, another ball (w=g(x) close enough to g(a) ) is small enough that can be put into a ball f(x). Therefore, to get f(w) get arbitrarily close to f(g(a)). So it can provided f(g(x)) close enough to f(g(a)), f(g(X)) is continuous at a.
The distinguishes convergent sequence from divergent sequence.
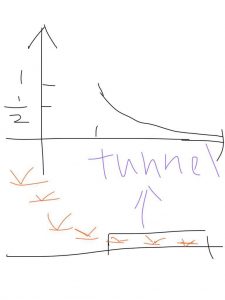
Consider a sequence as a group of birds they fly follow a certain line or curve,and there is a very small space which can be considered as a tunnel .To say a sequence converges, thats to say no matter how small the high of the tunnel is the first bird of its fly curve or line lead the group can toward inside it.To say a sequence diverges,thats to say they fly as high as they want ,and the w first one of birds refuses to fix their line in a small space(the small tunnel), therefore, they fly randomly or fly higher as they like.
Example:sequence 1/n converges.
1The distinguish convergent series from divergent series.
Assume that a number in a series is not a point but is a space like a box,every box shows the magnitude of the sum of that part.Imagine we have a room with fixed space.If people can move all those boxes inside that room no matter how many the boxes are without beyond the room,we can say those space sums of those boxes are close to a fixed number and the series converges.Otherwise, those box can not be but in a fixed space room ,the sum of their space are bigger than the room has and it when numbers of boxes increase ,the sum increases,too.Therefore ,in this condition, we can say the series diverges.
Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!