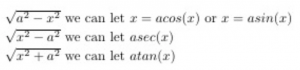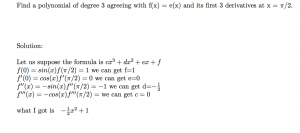In this assignment, I was asked to introduce an math idea in course.
I would like to introduce integration. Integration is a mathematical way to add all the small composition together to calculate a big things. For example, when you wanna calculate the area of a irregular graph, we cant just use some formula like calculate rectangle. The way we can is to use integration, divide the graph into infinite pieces and add those small areas together to whole area. This is the way called integration.
Time flies, two terms are all gone now. We have learned two courses of math: math100 and 101. It seems a little bit difficult for me, but it help us make a big progress in math learning. For me, after being inspired by Fok, I’d like to choose math as specialization for second year. I do really like Fok teaching style.
What impress me most is the way of thinking math. Previously, I think math is boring and is just to calculate stuffs, while Fok totally change my mind by now. He always can find some interesting examples to attract our ideas. In other way, he can put math relate to our life and make us think it funny and useful. For instance, in the latest lecture, he compare love with engine factor&value or null-clines. It sounds really hard and complicated at workshop for us. After his creative comparison, it became easy to understand and really interesting. I know math is not just for fun, but the way he thinking and teaching impress me a lot. I find out everything is can be full of fun which all depend on the way you think it. And I notice that creativity is an really important factor.