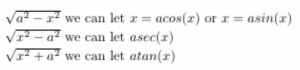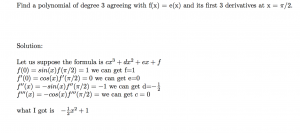In this assignment, I was asked to introduce an math idea in course.
I would like to introduce integration. Integration is a mathematical way to add all the small composition together to calculate a big things. For example, when you wanna calculate the area of a irregular graph, we cant just use some formula like calculate rectangle. The way we can is to use integration, divide the graph into infinite pieces and add those small areas together to whole area. This is the way called integration.

Time flies, two terms are all gone now. We have learned two courses of math: math100 and 101. It seems a little bit difficult for me, but it help us make a big progress in math learning. For me, after being inspired by Fok, I’d like to choose math as specialization for second year. I do really like Fok teaching style.

What impress me most is the way of thinking math. Previously, I think math is boring and is just to calculate stuffs, while Fok totally change my mind by now. He always can find some interesting examples to attract our ideas. In other way, he can put math relate to our life and make us think it funny and useful. For instance, in the latest lecture, he compare love with engine factor&value or null-clines. It sounds really hard and complicated at workshop for us. After his creative comparison, it became easy to understand and really interesting. I know math is not just for fun, but the way he thinking and teaching impress me a lot. I find out everything is can be full of fun which all depend on the way you think it. And I notice that creativity is an really important factor.

I was asked to do more deeper question related to question 2 in the assignment.

For instance f(x)=sin(x) and g(x)=e^x, f(x) is analytic at c, and g(x) is not.

A function analytic at c means this function convergent power series for x=c. And only if Taylor series for particular function converge to this function for every single c at x=c.

Analytical functions are supposed to be infinite differentiable. It does not mean all the infinitely function is analytic, such as y=e^(-c)cos(cx).

The reason for its usefulness is that if we know that a function is analytic when x=c, we can get power series at x=c in domain.

I did really bad in this midterm. I was not careful about the webwork question and in classes I seldom took notes in this first half of term. My tips is obvious that we are supposed to do all the webwork problems carefully and listen to big and lecture carefully. Be sure to take notes in class and review them later.
The last question of first problem is the most difficult question of the whole exam. The question is evaluate integration 1/t^2sqrt(t^2+1) from 1 to sqrt(3). The reason is that two substitution are needed for the question. And we have to be familiar with sec and tan which we did not always use it in high school.
In the last half of the term, I will try hard and get a good marks in the final.

1.
In trigonometric function, many cases can make two square of things equal to a constant. So we can use trigonometric function as constitution when two factor are square.

2.
You can try to substitute many different value, then compare the next part and choose the easy one.

3.
Do not always try to use constitution to solve the problem, sometimes other way may be better.

From the definition, we know that if exist and have same upper bound and lower bound when the selecting point changing.Coz there will be some bad subinterval happen, but we know the number of it is countable. It does not matter after we divide the function into n which is large enough parts. The upper bound will become smaller and smaller, and the lower bound will become bigger and bigger until they become the same.Which means if the removed points is not infinity , the function still integrable.

In this assignment, I am asked to write a question for the final test.So I just rewrite an question from assignment. Though it’s not that hard but it’s really important and basic.

The fountain in UBC is a good example. As we all know, the water will pour into the fountain through the pipes. Let us assume that there are 20 pipes in the fountain and each of it pour 0.05L/s . The area of the fountain is 20 square metre. The question is rate of depth of the fountain.
This question is easier than the given one , because the fountain is regular which means its area won’t change with depth.
Here is the solution. 20pipes can pour 20*0.05=1L per second.According to the density of water , 1L water equal to 0.001 cubic metre, V(D)=0.001m^3/20m^2=5*10^-5m=0.05mm per sec

Today I am asked to convince you the intermediate value theorem, and I’d like to use some simple example in our daily life to make it.I believe the running in a filed can make sense.
Mike is a runner who always run after class. He always run 200m in 5min every day.Let the 200m track is straight or curl whatever.But if Mike need to reach the end of the track, he must go through the each point of the track in some time during the 5min, even though the track is longer than 200m and you surpass the end of the track and go back at last .Coz the Mike cannot fly or something like take a cab to prevent you from going through the any point of 200m to reach the end.
As the intermediate value theorem
—–{if a continuous function f with an interval [a, b] as its domain takes values f(a) and f(b) at each end of the interval, then it also takes any value between f(a) and f(b) at some point within the interval.}
Each point is the f(x) in the theorem and the time is the x in it.The the f(x) must go through all the value before he get the f(b).So the theorem hold water.

I can not print some mathematic words here, so i would like to use a photo instead to show the math in our daily life. xD

Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!