After a flourishing period of melatonin manufacturing, hundreds of brands with doses range from 2 mg to 10 mg per tablet are available over-the-counter without a prescription. It is common for some people live in USA and Canada using melatonin for over 10 years. All stories between human and melatonin start since we exist – it is a natural excreted hormone in our body to regulate circadian rhythm. But humans really getting to know and use melatonin is from the last century, especially after it being allowed to be sold as a dietary supplement by Health and Education Art since 1994 in USA.

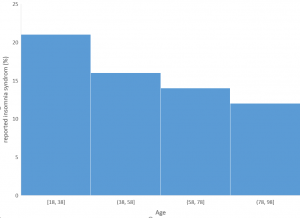
Chart 1. Number of Received Reports vs Initial Received Time

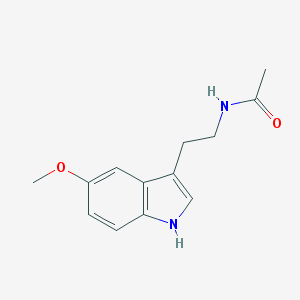
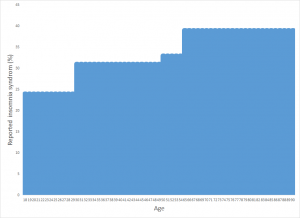
Based on 47 serious adverse reactions reports during 1994-01-01 to 2018-06-30 retrieved from Canada Vigilance Adverse Reaction Online Database on Health Canada, overdosing on melatonin could result in anxiety, depression, blood pressure increased, coma and so on. A great increase of reports shows up after 2011. There is no remarkable difference among 4 generations (realized generational interval = 21 years).

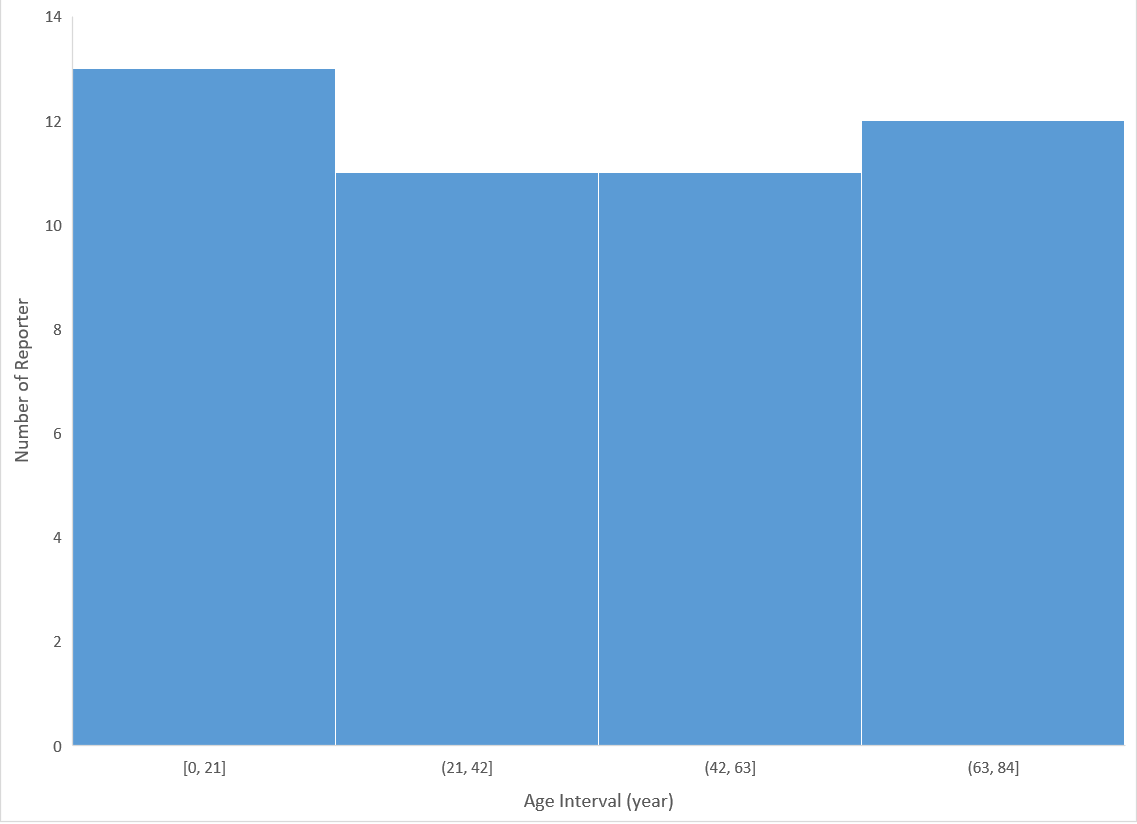
Chart 2. Reporter Partition vs Age (generational interval = 21)

Unlike the North Americans, Europeans are stricter with oral supplementation of this “timing hormone”. Denmark and Czech Republic prohibit melatonin as a food supplement. In UK, pharmacies ask for prescriptions from people who purchase melatonin. Manufacturers in Belgium and Germany provide their products with low dose at 0.3 mg for daily use and higher dose for special medicinal purpose. Spain and Italy limit the daily dosage at 1 mg while physiological efficacy is retained.

Interestingly, according to Natural Health Products Ingredients Database from Health Canada, oral melatonin is applicable to adults 18 years and older with daily dose from 0.1 – 10 mg for non-jet lag uses and 0.5-10 mg for jet lag. No label notifies the restricted use of melatonin on the minority.

Figure 1. Surface Label of Commercially Available Melatonin

The database also warns the uncertain safety of long-term use and possible physiological hazards with alcohol and other drugs and mental sedation. Manufactures avoid mentioning those cautions in advertising though they print those in the relatively small font on the hidden label in which customers have to remove the cover indicated by ”PEEL HERE” in the corner.

Figure 2. The Hidden Label with Cautions and Warnings

Continue reading →

Melatonin (IUPAC name: N-Acetyl-5-methoxytryptamine), known as a neurohormone synthesized at pineal gland and narcotically excreted to regulate circadian rhythm and sleep, is easily available at health food stores and retail pharmacies over-the-counter without prescriptions. insomnia is a sleeping disorder which is characterized by either having difficulty in falling asleep or being awake easily during the night.

Atomic model of N-Acetyl-5-methoxytryptamine

line-bond Structure of N-Acetyl-5-methoxytryptamine

increasing reported insomnia syndrome with aging

The secretion of melatonin decreases with aging while this could explain why sleeping problems seem to be more common among the elders. The database from 2005 National Sleep 

Foundation poll shows this trend as the reported insomnia syndrome partition increase with increasing age.

decreasing reported insomnia syndrome with aging

However, this trend is flipped over when a different partition of ages is applied. Instead of seperating the age of voters into [18,29],[30,49],[50,54],[65+], with new age partition we can see people before middle age(<=38) actually are reported as highest partition bothered by insomnia syndrome. pressure and stress.

Easy accessibility of melatonin may lead to abuse or overdose though its toxicity is tested as low, whereas the case study of melatonin is still limited and no assembly analysis of negative effects of melatonin use is published.

According to past study, three cases of using melatonin for suicide attempts are not harmful while in all cases the doses are less than 150mg per time. While another study aimed at long-term use and overdose intake show the significant relationship in worsening depression.

(Try to search the information as much as possible one could(do not let it be overwhelmed)

Appendix: website

COURSERA: https://www.coursera.org/

Xuechen Mi 24050163

The Difference and Connection between Antiderivative and Integral

The antiderivative is the inverse process of the derivative.The integral is to calculate the area closed by the graph of a function and x(or y) axis. However, Newton-Leibniz connect antiderivative and integration by giving a formula:∫^a_bf (x) dx = F(b)−F(a). In some cases, the integral of function f(x) on closed interval [a,b] can be calculated from the difference of its bounds’ antiderivative[(F(a)-F(b)]. When we do the calculation of antiderivative, we come up with a formula with an inconstant instead a definite value, which is the outcome of integral. A continues function must have its antiderivative. A function with first discontinuous points does not have its antiderivative.

Antiderivative and integral are two different things: if on interval[a,b], F’(x)=f(x), we can say F(x) is one of antiderivatives of f(x) on this interval. Based on this case, if F(x) is one of antiderivatives of f(x), F(x)+C(C is a random constant) is antiderivative of f(x). Then if f(x) is able to be integrated on [a,b], it may not have antiderivative. If f(x) is continuous on [a,b], f(x) constantly has its antiderivative G(x) and G(x) is its upper limit function: F(x)=∫^x_af(t)dt+C

In fact, the antiderivative equals indefinite integral. A continuous function can have infinite antiderivatives, but can have only 1 definite value of integral(interval must be given).

The Motivation of Integration

    When you drive to work every day, have you ever think about how does your driving speed affect the time you spend on the road? You may think: well, it’s super simple the question.My house and the office building cannot walk so the distance will never change. When I drive faster, the time it takes me on the road is shorter than that when I drive slower. Like the lower-upper level relation between you and your boss, the distance you daily drive is the lower level of the exact speed of your car. That means the speed determine how the distance work as your boss determine how you work.

    Once you are given a task from your boss, generally you should break the task into many small parts. It’s easy to manipulate most of the things step by step. Let us roughly and simply break the task into three steps: the first step to begin, the second step to work for the goal and the third step to close. As long one of these three steps has been done in order, 20%, 80%, 100% of the process are completed separately. The complement of each step needs time to be pushed forward. But if we add up all these parts, the time goes on and the process is accumulating, then the whole task will be done which means you can earn your salary even can hear a raise from your boss. Actually, we can see the speed and distance work in a similar way: the engineer pushes your car in three constant speed. Going with different driving speed and flowing time, the street runs behind you. Finally, you either catch up on time or come late and lose the attendance bonus (sad). Whatever, the car has finished the aimed mileage, its task.

The sum up of stepped speed shows the distance. The boss determines how much work you should do. The upper level instructs lower level. The lower level in some fields is not easy to manipulate. At that time, we ought to focus on the upper level, because it provides a clearer overview of what is going on now in the lower level.

To do with part a), we are given 4 graphs presenting the change and regularity of Sierpinski carpet. From these graphs, we can see and find the value of each p1,p2,p3, then deduct the general formula. (The whole construction follows the general formula shown in initial several steps)

To do with part b), find the relationship between what we have and what we want. We write the p_n we get from a) in the standard formation of its series type. p_n is the geometric series, and it can be written as  a*q^{n-1}, then just plug it in the relationship we establish.

in part c), we find the limit in we get the answer in part b). To reject the answer in b, we can abandon the  limit which makes area equals 0, so the equation is not satisfied, the requirement of c satisfies.

a)  SEQUENCE is a list of numbers in order.When we say one sequence is convergent, we have lim a_n (n approach to infinity) equals a defined number. For example, a_n=n/(n+1), lim a_n =1, 1 is the constant. when n becomes larger and larger, a_n can be as close as possible to 1, sequence {a_n} is convergent . When we say one sequence {a_n} is divergent, we can not define the exact value of a_n when n approaches  infinity. a_n=n, lim a_n = ∞ . The difference between divergent and convergent sequence can be found out by proving the sequence formula that whether it is infinite or finite.

b)SERIES can seem as the sum of infinite terms of a sequence. To find whether it is convergent or divergent, it does not work if we just see whether the sequence converges or diverges. When we say a series is convergent, we have a sum of {a_n}(n approaches infinity) is bounded. Whatever how many terms you add up, the value of series can only locate in bounded intervals. Like an=1/(n^2), lim sum of {a_n}=log2, the value is bounded above log2. Or we have divergent series, we have a sum of {a_n}(n approaches infinity) is without limit.  Like an=1/n, lim sum of {a_n}=∞, the value can be as large as possible with the increase of term.

Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!