Stephens and Clements (2015) discuss the importance of students having sufficient background foundational knowledge before exploring and utilizing simulations. Simulations help to motivate students and create excitement, but students need to understand that there is a difference between reality and simulation which was discussed by Srinivasan et al. (2006). This lesson will be using the T-GEM framework and an interactive activity from Illuminations. Using interactive manipulatives are helpful for learners as it allows these students to work at their own pace, self-discovery and exploration. The activities can be adapted to the individual learner with the support of the teacher if needed. Further using technology allows for an engaging and interactive learning experience for students. It’s also important for student to be able to connect curriculum to real life scenarios, and technology allows students to make these connections.
https://illuminations.nctm.org/Activity.aspx?id=3510
G-Generate:
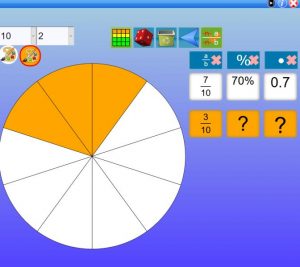
Exploration is key for students. This will allow students to ask questions they may have, and connect previous knowledge with knowledge they are gaining through self-discovery. Students will be able to practice the relationships between equivalent fractions and match each fraction to its location on the number line.
Students will use the interactive activity to explore. They will select “Build Your Own” option. Here students will be able to explore creating equivalent fractions by dividing and shading either circles or squares.
With students, go over key terminology and foundational concepts.
What are fractions?
What is a number line?
What is the numerator and what is the denominator?
What are the various ways to represent fractions?
Where do we use and see fractions in our everyday lives?
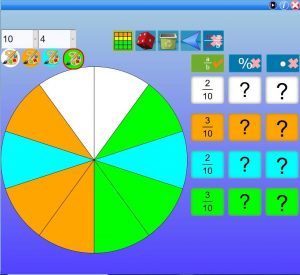
Students will generate a hypothesis regarding the relationships between fractions and how to create equivalent fractions and the relationship on the number line.
E-Evaluate:
During this stage, the teacher can pose questions that may not follow students’ hypotheses as this will allow students to evaluate the relationship. Teacher will also use equivalent fractions and have students create additional equivalent fractions. Here, students will have to use their numeracy skills to solve these questions.
M-Modify:
Teachers will ask students to represent fractions in lowest terms. Here students will have to use their multiplication and division skills to determine this relationship and apply their knowledge. How will students use their foundational knowledge and apply it to this activity.
Questions for students:
Can all fractions be reduced to lowest terms? What are the main “benchmark” fractions?
Can one fraction have many equivalent fractions? How can you show this visually and numerically?
How does multiplication and division relate to fractions? How are number lines useful to describe fractions?
Khan, S. (2010). New pedagogies for teaching with computer simulations. Journal of Science Education and Technology, 20(3), 215-232.
Srinivasan, S., Perez, L. C., Palmer,R., Brooks,D., Wilson,K., & Fowler. D. (2006). Reality versus simulation. Journal of Science Education and Technology, 15(2), 137-141.
Stephens, A. & Clement, J. (2015). Use of physics simulations in whole class and small group settings: Comparative case studies. Computers & Education, 86, 137-156.